[Algorithm] 01.Introduction to Algorithms + Basic Concepts of Sorting & Complexity

Introduction to Algorithms

알고리즘
특정 문제(problem)를 해결하는 잘 정의된 절차(procedure)
Procedure: instruction(명령)의 유한한 집합 Problem: 잘 명시된 input/output

Question to Answer

1. Description
   알고리즘이 어떻게 동작하는지
2. Correctness
   알고리즘이 정확한 output을 만들어내는지
3. Performance
   알고리즘이 얼마나 효율적으로 동작되는지
   1) Time Complexity
   2) Space Complexity

Importance of Efficient Algorithms
만약 A라는 컴퓨터가 1초에 $10^{10}$ 개의 instruction을 실행하고,
B라는 컴퓨터가 1초에 $10^{7}$ 개의 instruction을 실행한다고 했을 때,
당연히 B 컴퓨터가 성능이 안 좋을 것을 알 수 있다.
하지만, 알고리즘 1이 $2n^2$ 개의 instructions이 필요하고,
알고리즘 2가 $50 \times n \lg n$ 개의 instructions가 필요할 때,
알고리즘 1을 A 컴퓨터에, 알고리즘 2를 B 컴퓨터에서 동일하게 $10^7$개의 instruction을 돌린다면, 아래와 같은 결과를 도출할 수 있다.

\[A: \quad \frac{2 \times (10^7)^2}{10^{10}} = 20000 \, sec \qquad B: \quad \frac{50 \times 10^7 \lg 10^7}{10^{7}} \approx 1163 \, sec\]

성능이 안 좋은 B 컴퓨터라도 효율적인 알고리즘을 짠다면, 효율적으로 Computing할 수 있다.

Sorting Problems

Sorting Problem이란 특정한 순서로 elements(요소들)의 시퀀스를 재배열하는 것

Input
n개의 숫자 시퀀스

Output
input sequence에 대해 재정렬된 permutation

Sorting의 장점

1. 리스트에서 특정한 값을 찾기 쉬워짐
2. 리스트에서 min/max나 k번째 작은/큰 값을 찾기 쉬워짐
3. 리스트에서 중복되는 값을 삭제하기 위해 특정 item에 대한 uniqueness를 체크하기 쉬워짐
4. 특정 값이 몇 번 등장하는지 세기 쉬워짐
5. 금융 거래 내역 정렬 등

즉, 복잡한 문제를 풀기 위한 중간 단계로서 많이 활용하기에 Computer Science에서 매우 기초적인 연산이라고 할 수 있음

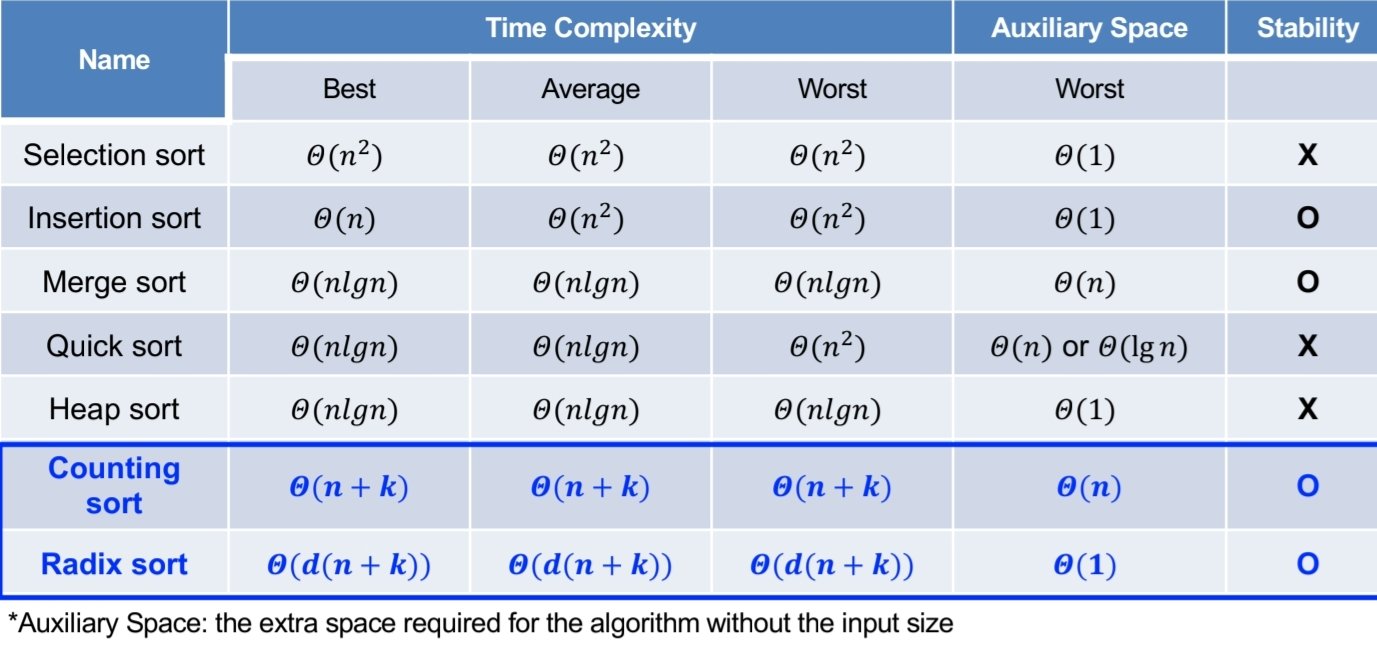
Sorting 알고리즘의 분류와 영향을 주는 요소(Factors)

1. Comparison-based Algorithms
   => Bubble sort, Insertion sort, Selection sort, Merge sort, Quick sort, Heap sort, …
2. Non-comparison-based Algorithms
   => Counting sort, Radix sort, …

특정 application에서 가장 좋은 알고리즘을 고르는 것은 Element-related factor와 Element-unrelated factor에 의존함
1) Element-related factor: elements가 이미 정렬된 정도, element 값에 대한 제한 등
2) Element-unrelated factor: 컴퓨팅 디바이스(CPU, GPU 등), 스토리지 디바이스(SSD, HDD 등)

Insertion Sort(삽입 정렬)

A sorting algorithm repeatedly inserting a ‘key’ element from the unsorted portion of the list into the sorted portion of the list while preserving the sorted order
정렬된 순서는 유지한 채, 리스트의 정렬되지 않은 부분에서 정렬된 부분으로 key element를 반복적으로 삽입하는 정렬 알고리즘

key element는 정렬 순서에 따라 적절한 위치에 삽입된 후 다음 인덱스로 이동된다.

Pseudo Code of Insertion Sort (Non-decreasing)

INSERTION-SORT(A)
  for j=2 to A.length
    key = A[j]
    //Insert A[j] into the sort sequence A[1 ~ j-1]
    i = j-1
    while i > 0 and A[i] > key
      A[i+1] = A[i]
      i = i - 1
    A[i+1] = key

Correctness of Insertion Sort

A[0, 1, …, i-1]이 항상 특정 순서로 정렬되었다는 것을 보장할 수 있다.
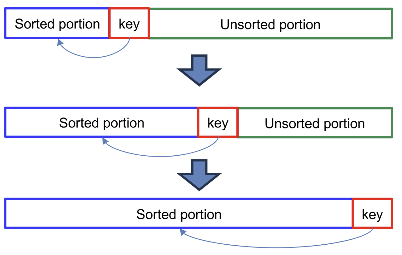
위 Pseudo Code를 살펴보았을 때, ㅁ 아래 그림의 파란색 부분은 while문, 빨간색 key 부분은 key=A[j]와 대응하는 것을 확인할 수 있고,
점차 step을 반복하면서 unsorted가 sorted로 바뀌면서 모든 요소가 정렬되는 것을 확인할 수 있다.

Pseudo Code of Insertion Sort (Non-increasing)

INSERTION-SORT(A)
  for j=2 to A.length
    key = A[j]
    //Insert A[j] into the sort sequence A[1 ~ j-1]
    i = j-1
    while i > 0 and A[i] < key
      A[i+1] = A[i]
      i = i - 1
    A[i+1] = key  

쉽다. 위에서 제시한 코드에서 A[i]와 key의 비교만 부등호 방향을 바꿔주면 된다.

교재 예시 문제(2.1 - 3)

Searching Problem.
Input: n개의 숫자 시퀀스인 A와 v라는 값
Output: 인덱스 i 또는 NIL (v가 A에 없을 때)
linear search로 pseudocode를 작성.

LINEAR_SEARCH(A, v)
  for i=1 to length(A)
    if A[i] == v
      return i
  return NIL

교재 예시 문제(2.1 - 4)

n-bit binary integer 두 개를 더하는 문제. n-element인 A와 B에 각각 저장되어 있고, (n+1)-element 배열인 C에 그 결과를 저장하는 Pseudo Code 작성

BINARY_ADD(A, B, n)
    Let C be an array of size (n+1)
    carry = 0
    for i = n-1 down to 0  // Start from LSB (rightmost bit)
        sum = A[i] + B[i] + carry
        C[i+1] = sum % 2     // Store the binary sum (0 or 1)
        carry = sum / 2      // Compute carry for next step
    C[0] = carry            // Store final carry in the MSB position
    return C

Implementation Insertion Sort in Python(Non-decreasing)

def insertion_sort(arr):
    n = len(arr)
    for j in range(1, n):
        key = arr[j]
        i = j - 1
        while i >= 0 and arr[i] > key:
            arr[i + 1] = arr[i]
            i -= 1
        arr[i + 1] = key  # Place key in correct position
    return arr

Performance Evaluation

알고리즘이 효율적으로 동작하는지 파악하기 위해 Performance Measurement를 할 필요가 있지만, 실행 시간은 대부분 machine-dependent한 요소이기 때문에, Performance Analysis를 진행하고, 이는 Machine-independent하다.
알고리즘이 실행하는 instruction의 개수를 셈으로써 분석하는 과정으로, Time Complexity와 Space Complexity가 있다.

Time Complexity of an Algorithm

특정한 input에 대해 알고리즘에서 실행된 기본 instruction의 개수
즉, 얼마나 많은 instruction이 실행되는지가 Time Complexity(=Running Time)을 결정한다.

여기서 primitive instruction이란, Arithmetic(산술), Data Movement(데이터 이동. 예: load, store, copy 등), Control 등에 이용하는 instruction을 말한다.

예를 들어서, Prefix Average 관련 함수가 아래와 같이 제공될 때,

\[PreAvg[j] = \frac{\sum_{i=0}^{j}A[i]}{j+1}\]

void prefixAverage(int A[], int PreAve[], int n){
    for (int j=0; j<n; j++){        //c_1
        int sum = 0;                //c_2
        for (int i=0; i<j+1; i++){  //c_3
            sum += A[i];            //c_4
        }
        PreAve[j] = sum / (j+1);    //c_5
    }
}

\(c_1 \times (n+1) + c_2 \times n + c_3 \times (\frac{n(n+1)}{2}+1) + c_4 \times (\frac{n(n+1)}{2}) + c_5 \times n\)

Quadratic Time 즉, 이차식으로 구성된다.

비효율적인 코드. Linear Time으로 코드 수정할 수 있다.

void prefixAverage(int A[], int PreAve[], int n){
    int sum =0;                     //c_1
    for (int j=0; j<n; j++){        //c_2
        sum += A[j];                //c_3
        PreAve[j] = sum / (j+1);    //c_4
    }
}

\(c_1 \times 1 + c_2 \times (n+1) + c_3 \times n + c_4 \times n\)
\((c_2+c_3+c_4)\times n + (c_1+c_2)\)

cf. return문은 1번 실행되므로 1로 카운트한다.

Complexity Analysis: Insertion Sort

실제로 앞서 살펴본 Insertion Sort의 Time Complexity를 계산해보자.

INSERTION-SORT(A)
  for j=2 to A.length           //c_1
    key = A[j]                  //c_2
    //Insert A[j] into the sort sequence A[1 ~ j-1]
    i = j-1                     //c_3
    while i > 0 and A[i] > key  //c_4
      A[i+1] = A[i]             //c_5
      i = i - 1                 //c_6
    A[i+1] = key                //c_7

$t_j$: 변수 j에 대하여 while loop를 도는 횟수

\[c_1 \times n + c_2 \times (n-1) + c_3 \times (n-1) + c_4 \times \sum_{j=2}^{n}t_j + c_5 \times \sum_{j=2}^{n}(t_j - 1) + c_6 \times \sum_{j=2}^{n}(t_j - 1) + c_7 \times (n-1)\]

그렇다면 best 케이스와 worst 케이스를 나눠 살펴보자.

Best-case
이미 정렬된 배열이다.
$c_5 \times \sum_{j=2}^{n}(t_j - 1) + c_6 \times \sum_{j=2}^{n}(t_j - 1)$가 사라진다.($t_j$가 1이기 때문)
따라서, $T(n)=(c_1+c_2+c_3+c_4+c_7)\times n - (c_2+c_3+c_4+c_7)$
n에 대한 Linear function이 나온다.

Worst-case
역으로 정렬된(내림차순으로 정렬된) 배열이다.
$t_j$가 j이기 때문에, $c_5 \times \sum_{j=2}^{n}(t_j - 1) + c_6 \times \sum_{j=2}^{n}(t_j - 1)$가 n에 대한 이차식으로 등장하게 되고,
$\sum_{j=2}^{n}t_j = \frac{n(n+1)}{2}-1$이고, $\sum_{j=2}^{n}(t_j - 1) = \frac{n(n-1)}{2}$이기 때문에,
최종적으로 n에 대한 Quadratic function이 나온다.

즉, 정리하면, input size가 동일하더라도, 알고리즘의 실행 시간이 Best, Avg, Worst 케이스에 따라 바뀔 수 있다는 것이다.

Three Types of Time Complexity Analysis

1. Best-Case Analysis
2. Average-Case Analysis
3. Worst-Case Analysis

오로지 Worst-Case Analysis를 함. 왜? 실용적 관점에서 유용하기도 하고, upper bound(상한선)을 제공해주며, 실제 application에서 worst-case가 빈번하기도 한데, average-case가 worst-case랑 time complexity가 동일한 경우가 꽤 많기 때문!

cf. Space Complexity of Insertion Sort

=> In-place sorting algorithm, 상수 공간(즉, 변수 할당만을 위한 메모리 공간)만 필요하기 때문이다.

Asymptotic Analysis(점근적 분석)

input size가 커짐에 따른 알고리즘의 growth rate를 평가하는 것

Complexity Analysis의 역할

1. 알고리즘의 효율성에 대한 간단한 characterization 제공
2. 다른 알고리즘에 대한 상대적 성능 비교를 가능하게 함
3. 더 큰 input size에서 알고리즘이 어떤 성능을 보이는지 예측 가능하게 함

Asymptotic Notations

1. $O$-Notation
   간단한 표현: \(f(n) = O(g(n)) \approx f(n) \leq g(n)\)
   정의: 모든 $n \geq n_0 > 0$에 대하여 $0 \leq f(n) \leq c \times g(n)$ 인 양의 상수 $c$와 $n_0$가 존재하면 $f(n) = O(g(n))$
   목표하는 알고리즘(f)의 시간복잡도가 g보다 작거나 같음, 즉, 최악의 경우를 나타낸다.
   f(n)의 점근적 상한선 (Asymptotic Upper Bound)가 g(n)이다라고 표현한다.
   실제 증명 문제에서는, $c$나 $n_0$ 값에 대한 범위를 표시해주는 게 일반적이다.
2. $o$-Notation
   간단한 표현: \(f(n) = o(g(n)) \approx f(n) < g(n)\)
   정의: 모든 $n \geq n_0 > 0$에 대하여 $0 \leq f(n) < c \times g(n)$ 인 양의 상수 $c$와 $n_0$가 존재하면 $f(n) = o(g(n))$
   Big O는 무한대로 커질 때 뿐만 아니라 특정 값에 가까워질 때에 대해서도 사용할 수 있었지만(some positive constants 에 대해서만 만족해도 됨), Little o는 무한대로 커질 때만 사용되는 개념(all positive constants 에 대해서만 만족)
   $\lim_{n \to \infty} \frac{f(n)}{g(n)} = 0$
   Asymptotically tight한 경우는 Big-O는 만족하지만 Little-o는 만족하지 않는 경우이다.
3. $\Omega$-Notation
   간단한 표현: \(f(n) = \Omega(g(n)) \approx f(n) \geq g(n)\)
   정의: 모든 $n \geq n_0 > 0$에 대하여 $0 \leq c \times g(n) \leq f(n)$ 인 양의 상수 $c$와 $n_0$가 존재하면 $f(n) = \Omega(g(n))$
   목표하는 알고리즘(f)의 시간복잡도가 g보다 크거나 같음, 즉, 최선의 경우를 나타낸다.
   f(n)의 점근적 하한선 (Asymptotic Lower Bound)가 g(n)이다라고 표현한다.
4. $\omega$-Notation
   간단한 표현: \(f(n) = \omega(g(n)) \approx f(n) > g(n)\)
   정의: 모든 $n \geq n_0 > 0$에 대하여 $0 \leq c \times g(n) < f(n)$ 인 양의 상수 $c$와 $n_0$가 존재하면 $f(n) = \omega(g(n))$
   Big-$\Omega$는 무한대로 작아질 때 뿐만 아니라 특정 값에 가까워질 때에 대해서도 사용할 수 있었지만(some positive constants 에 대해서만 만족해도 됨), Little-$\omega$는 무한대로 작아질 때만 사용되는 개념(all positive constants 에 대해서만 만족)
   $\lim_{n \to \infty} \frac{f(n)}{g(n)} = \infty$
   Asymptotically tight한 경우는 Big-$\Omega$는 만족하지만 Little-$\omega$는 만족하지 않는 경우이다.
5. $\Theta$-Notation
   앞서 다룬 Big-O나 Big-$\Omega$가 의미가 있지는 않다. 해당 알고리즘의 tight한 bound를 알 수가 없기 때문이다.
   간단한 표현: \(f(n) = \Theta(g(n)) \approx f(n) = g(n)\)
   정의: 모든 $n \geq n_0 > 0$에 대하여 $0 \leq c_1 \times g(n) \leq f(n) \leq c_2 \times g(n)$ 인 양의 상수 $c_1$, $c_2$와 $n_0$가 존재하면 $f(n) = \Theta(g(n))$
   f(n)의 (Asymptotic Tight Bound)가 g(n)이다라고 표현한다.
   Theorm: For any two functions $f(n)$ and $g(n)$, we have $f(n) = \Theta(g(n))$ (Tight Bound) if and only if (필요충분조건) $f(n)=O(g(n))$ and $f(n)=\Omega(g(n))$
   Lesson: 다항식 p(n)에선 최고차항의 계수만을 고려함.,

Asymptotic Notation의 특성

1. Relational Properties (Transitivity, Reflexivity, Symmetry, Transpose symmetry)
2. Trichotomy(삼분법)
   어떤 실수 a, b를 선택했을 때 다음 세 관계 중 무조건 하나엔 해당해야 한다.
   1) a < b
   2) a = b
   3) a > b
   즉, 임의의 두 실수는 comparable (비교 가능) 해야 한다.
   하지만, 임의의 두 함수는 점근적으로 비교가능하지 않은 경우도 있다.
   Asymptotically Comparable이 아닌 경우 => $f(n)=n$, $g(n) = n^{1+\sin n}$