[Algorithm] 02. Divide & Conquer(1)-MergeSort

1. Divide & Conquer

1) 큰 규모의 문제를 작은 subproblem으로 나눈다. [Dividing]
2) 각 subproblem을 재귀적으로 해결한다. [Conquering]
3) 각 솔루션들을 합쳐서 원래 문제에 대한 솔루션을 만든다. [Combining]

Applications
Merge sort, Quick sort, Min/Max Finding, QuickHull, Strassen의 행렬 곱셈

장점

1. Simplicity: 이해하기 구현하기 쉽고 단순해짐
2. Efficiency: 일반적으로 merge/quick sort는 $O(n \lg n)$의 시간복잡도를 가짐
3. Parallelism: 쉽게 병렬화할 수 있어 빠름

단점

1. 메모리 사용량이 높음: 메모리를 많이 요구함(e.g. Merge sort도 Auxilary Space가 $\Theta(n)$이 필요)
2. Applicability가 낮음(= general하게 사용 불가능): 특정 TASK에 적합한 경우가 많음
3. 분석의 어려움: 시간/공간 복잡도를 분석하기 어려움 -> Recurrence 푸는 형태로 나타남

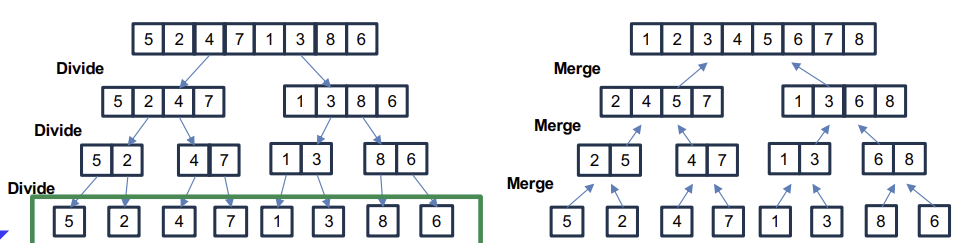
2. Merge Sort

1) input array를 두 개의 subarray로 나눈다. [Dividing]
2) merge sort를 활용해서 재귀적으로 각 half-size array를 정렬한다. [Conquering]
-> 배열 size가 1이면, 이미 정렬된 것으로 본다(base case)
3) 각 솔루션들을 합쳐서 원래 문제에 대한 솔루션을 만든다. [Combining]

Merge sort Psuedocode

MERGE-SORT(A, p, r)
if p < r
    q = |(p+r)/2|  
    MERGE-SORT(A, p, q)
    MERGE-SORT(A, q+1, r)
    MERGE(A, p, q, r)

MERGE(A, p, q, r)
n1 = q-p+1 // left-side subarray 크기  
n2 = r-q // right-side subarray 크기  
let L[1, ..., n1+1] & R[1, .., n2+1] // 새로운 배열 L, R을 생성
//L과 R에 element copy
for i=1 to n1
    L[i]=A[p+i-1]
for j=1 to n2
    R[j]=A[q+j]
L[n1+1] = $\infty$
R[n2+1] = $\infty$  
i=1
j=1
for k=p to r
    if L[i] <= R[j]
        A[k] = L[i]
        i = i+1
    else
        A[k]=R[j]
        j = j+1

중간에 센티널(sentinels) 사용하지 않고 MERGE 수도코드를 재작성하기

MERGE(A, p, q, r)
n1 = q-p+1 // left-side subarray 크기  
n2 = r-q // right-side subarray 크기  
let L[1, ..., n1+1] & R[1, .., n2+1] // 새로운 배열 L, R을 생성
//L과 R에 element copy
for i=1 to n1
    L[i]=A[p+i-1]
for j=1 to n2
    R[j]=A[q+j]
i=1
j=1
for k=p to r
    if i > n1
        A[k] = R[j]
        j = j+1
    else if j > n2
        A[k] = L[i]
        i = i+1
    else if L[i] <= R[j]
        A[k] = L[i]
        i = i+1
    else
        A[k] = R[i]

Correctness of Merge-sort
두 개의 정렬된 half-size subarray를 결합해서 정렬된 subarray를 얻는다.

Time Complexity of Merge Sort

머지 소트의 시간 복잡도는 Recurrence equation(점화식)으로 표현된다.

1. Divide
   D(n) = $\Theta(1)$
2. Conquer
   2 * T(n/2)
3. Combine
   C(n) = $\Theta(n)$

따라서, 다음과 같은 식을 얻을 수 있다.
\(T(n) = 2 \times T(n/2) + \Theta(n)\)
위 점화식을 풀기 위해서, Recursion Tree를 활용한다.

$\Theta(n)$이기 때문에 cn으로 나타낼 수 있고,
트리를 통해 /2된 값이 배로 늘어나서 결국 각 Lv의 합은 cn이 된다.
트리의 높이는 $\lg n + 1$이므로, 시간복잡도 T(n)은 결국 cn과 $\lg n + 1$의 곱으로 나타낼 수 있다.
따라서, $T(n)=\Theta(n \lg n)$

머지소트는 특이하게도 best case와 worst case 모두 $\Theta(n \lg n)$의 시간복잡도를 갖는다.

Merge-Insertion Sort: Improving Merge Sort

작은 input(=small problems)에서는 Insertion sort의 상수 계수들이 실제로 더 빠르게 동작할 수 있다.
그래서, 위 아이디어를 통해 Merge-Insertion Sort는 다음과 같은 동작을 함.

1. 동일하게 Dividing 해줌(subarray size가 k가 될 때까지 == n/k subarray가 있을 때까지)
2. 크기가 k인 subarray를 insertion sort를 통해 정렬
3. Merge sort로 정렬하며 병합(Merging)

그러면 Merge-Insertion Sort의 시간복잡도를 구해보자.

1. Sort과정: best인 경우는 $\Theta(k \times (\frac{n}{k})) = \Theta(n)$이며, worst인 경우 $\Theta(k^2 \times (\frac{n}{k})) = \Theta(nk)$이다.
2. Merge과정: worst case만 고려, level 개수와 각 level의 시간 복잡도를 곱해주면 된다. $\lg \frac{n}{k} \times \Theta(n) = \Theta(n\lg \frac{n}{k})$

정리하면,
Best-case: $\Theta(n) + \Theta(n\lg \frac{n}{k}) = \Theta(n\lg \frac{n}{k})$
Worst-case: $\Theta(nk) + \Theta(n\lg \frac{n}{k} = \Theta(n\lg \frac{n}{k})$

Merge sort나 Insertion sort에 비해 성능이 향상된 것을 확인할 수 있다.

3. Solving Recurrence

Divide & Conquer 알고리즘은 점화식의 형태로 표현된다.
아래 3가지 방법을 통해 점화식을 풀 수 있다.

1. Substitution method
2. Recursion-tree method
3. Master method

점화식을 푼다는 것은 solution에 대한 빅-세타, 빅-오 경계를 얻는 것이다.

Substitution method

1. Guess solution
2. 수학적 귀납법을 통해 guess를 증명하기

즉, 일단 T(n)이 무엇일지 예상하고, 이를 귀납법을 통해 증명하는 것이다.
예를 들면, 머지소트에서 $T(n)=\Theta(n \lg n)$임을 예상하고, $T(n) \leq cn \lg n \quad (c>0)$을 증명하는 과정을 생각해볼 수 있다.
하지만, tight bound를 잡을 수 없다는 점에서, Recursion-tree 방식을 활용해 tight bound를 구하고, 귀납법을 통해 증명하는 파트를 검산하는 용도로 주로 사용한다.

Recursion-tree method

1. Recursion Tree를 그림
2. 각 level에서의 cost 를 계산
3. Level의 개수 계산
4. 모든 level에서의 cost를 합산

여기서 height는 decreasing factor에만 적용받음

Master method

\(T(n) = aT(\frac{n}{b})+f(n)\)
위와 같은 꼴을 만족 시에 사용할 수 있다.
눈치챘다시피, $a \geq 1$는 subproblem의 개수이고, $b > 1$는 decreasing factor이다.
f(n)은 D&Q 시에 발생하는 cost이다. 높이도 일반화하면 $log_b n$으로 나타낼 수 있다.(decreasing factor인 b에 오로지 의존하는 값임을 확인할 수 있다.)
뿐만 아니라, 마지막 레벨($\Theta(1)$인)의 개수는 $n^{log_b a}$로 고정됨을 알 수 있다.
아래는 total cost이다.

\[\mathrm{Total: } \Theta(n^{log_b a}) + \sum_{j=0}^{log_b n - 1} a^jf(n/b^j)\]

Case 1: $f(n) < n^{log_b a}$
어떠한 상수 $\epsilon > 0$에 대해서, $f(n) = O(n^{\log_b a-\epsilon})$ 라면,
\(T(n) = \Theta(n^{log_b a})\)를 취한다.

Case 2: $f(n) = n^{log_b a}$
$f(n) = O(n^{\log_b a})$ 라면,
\(T(n) = \Theta(n^{log_b a} \lg n)\)을 취한다.

Case 3: $f(n) > n^{log_b a}$
어떤 상수 $\epsilon > 0$에 대해서, $f(n)=\Omega(n^{\log_b a+\epsilon})$이고, $c<1$인 어떤 상수 c와 충분히 큰 모든 n에 대해서, $af(\frac{n}{b})<cf(n)$라면,
\(T(n)=\Theta(f(n))\)을 취한다.

Master Method로 안 되는 경우가 있다.
$T(n)= 4T(n/2) + n^2 \lg n$
확장된 Master Method를 이용하면 풀린다. (나중에 시간날 때 서술할 예정)