[Algorithm] 03. Divide & Conquer(2)-QuickSort

Quick Sort

Description of Quick Sort

1. 두 개의 subarray로 배열을 partitioning 한다. [Divide]
2. Quicksort() 함수를 재귀적으로 호출하여 두 subarray를 정렬한다. [Conquer]
3. subarray가 이미 정렬되었다면, combine할 게 없다. [X Combinde]

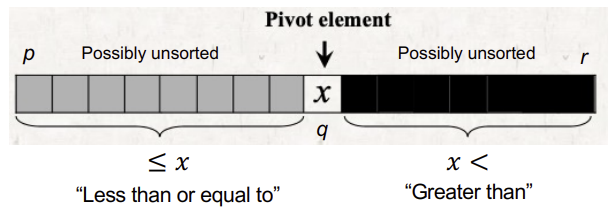
일반적인 퀵 소트에서 PIVOT을 마지막 또는 첫 번째 element로 선택한다.
cf. PIVOT(피벗)이란 기준이 되는 element로, 피벗 앞에는 피벗보다 작은 element들이, 피벗 뒤에는 피벗보다 큰 element들이 오도록 subarray를 나누는 기준이 된다. 피벗 자체는 subarray이 모두 채워지고 나서야 움직인다.

p: start index
r: end index
i: last index of the left subarray
j: current index

만약, A = [2, 8, 7, 1, 3, 5, 6, 4] 와 같은 배열이 있고, 마지막 원소인 4를 PIVOT으로 설정한다고 가정해보자.
p=0, j=0, r=7, i=-1 (i는 아직 left subarray가 생성이 안 되었기 때문에 -1로 두고, 모든 quick sort 코드에는 i=p-1로 설정한다.)

1) 첫 번째 원소인 2와 PIVOT 4를 비교한다. PIVOT보다 더 작으므로 left subarray에 해당 원소를 넣어줘야 하는데, 이 과정이 특이하다. i를 1 증가시키고, A[i]와 A[j]를 swap 해줌으로써 PIVOT보다 작은 값들의 subarray를 형성하고 키워나간다. 첫 번째 원소이므로, 2가 그대로 원래 자리에 위치하게 되며, p=i=0이 된다.
2) j를 1 증가시켜서 원소 8에 접근한다. PIVOT보다 크므로, 오른쪽 subarray에 포함되어야 한다. 하지만, 이때는 아무 원소도 움직이지 않는다. 그냥 current index인 j만 1 증가시킨다. 왜? i를 통해서 partition이 구분된다. 굳이 구분할 index 변수를 더 둘 필요도 없고, 다른 연산을 할 필요도 없다. 나중에 PIVOT 움직일 때도, 그냥 (i+1) 번째 원소랑 swap하면 된다.
3) j를 1 증가시켜서 원소 7에 접근한다. 마찬가지로 PIVOT보다 크므로 right subarray에 포함시킬 것이고, 추가적 연산없이 두면 된다.
4) j를 1 증가시켜서 원소 1에 접근한다. 1에서의 상황과 마찬가지로 PIVOT보다 작기 때문에 i를 1 증가시켜서 left subarray의 공간을 크기 1만큼 확장시키고, 그 자리에 존재하는 right subarray 소속의 원소와 swap한다. 당연히 right subarray 소속의 원소는 i가 1 증가해서 left subarray에 포함되었었지만 swap하면서 right subarray 오른쪽 끝으로 옮겨진다. 당연히 1증가된 i index 위치에는 1이 위치할 것이다.
5) 이런 과정을 나머지 원소들에 전부 거쳐 진행해주면, A = [2, 1, 3, 8, 7, 5, 6, 4]인 원소 배열 상태가 되며, p=0, i=2, r=7 (j는 loop문과 함께 이미 배열 index 범위를 넘어갔다.)
6) 마지막으로 PIVOT을 (i+1) 번째 원소인 8과 swap 함으로써 퀵 소트 정렬을 한다. 그 결과는 A = [2, 1, 3, 4, 7, 5, 6, 8]이다.

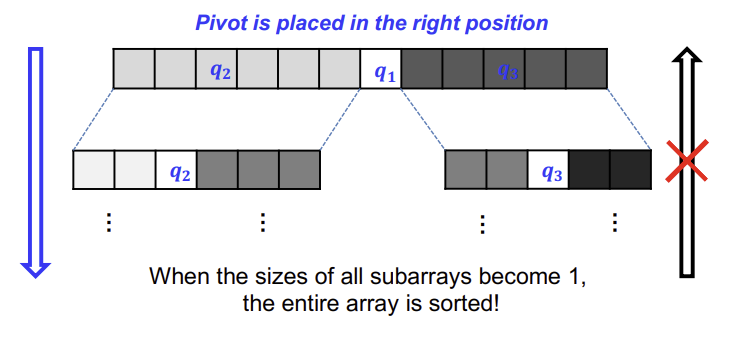
QUICKSORT(A, p, r)
  if p<r
    q = PARTITION(A, p, r) // 여기서 q는 i+1번째 index를 반환한다.  
    QUICKSORT(A, p, q-1)
    QUICKSORT(A, q+1, r)

PARTITION(A, p, r)
  x = A[r]
  i = p-1
  for j=p to r-1
    if A[j] <= x
      i = i + 1
      swap(A[j], A[i])
  swap(A[i+1], A[r])
  return i+1

Correctness of Quick Sort

잘 sorting 되는 걸 알 수 있다.

Complexity Analysis of Quick Sort

Quick Sort의 Time Complexity는 오로지 partitioning이 balance 한지 아닌지에 의존한다.

그러면 Partitioning의 worst-case와 best-case는 어떻게 될까?

1. Worst-Case Partitioning
   두 개의 subarray 내의 element 개수가 0개와 n-1개로 한쪽에만 쏠린 경우
   Recursion-Tree Method를 활용해 시간복잡도를 추정해보면
   \(T(n)=T(n-1)+T(0)+\Theta(n)=T(n-1)+\Theta(n)\)
   결국엔 $T(n)=\frac{n(n+1)}{2}$을 따라가고, $T(n)=\Theta(n^2)$임은 너무 자명하다.
2. Best-Case Partitioning
   두 개의 subarray 내의 element 개수가 정확히 절반으로 나뉜 경우
   \(T(n)=2T(n/2)+\Theta(n)\)
   딱보면 Recursion Tree에서 각 Lv 내 노드 합이 n으로 유지, 높이는 $\lg n$을 따라가므로, $T(n)=\Theta(n \lg n)$는 너무 자명하다.

그렇다면, Avg-Case Partitioning은 어떻게 구할까?
결론부터 설명하자면, Best-Case에 가깝다.
예를 들어, $T(n)=T(9n/10)+T(n/10) + \Theta(n)$라 했을 때,
양쪽 partitioning이 9:1로 나뉘는 것을 확인할 수 있고,
Recursion-Tree 그려보면, unbalanced 해보이지만, 여전히 $O(n \lg n)$를 만족함을 알 수 있다.
1:99 처럼 굉장히 치우쳐도 여전히 시간복잡도는 $O(n \lg n)$을 만족한다.

Worst-case inputs에 대한 상황은 얼마나 자주 발생하는가
만약, PIVOT의 설정을 Randomizing 해놓는다면,

1. 정확히 절반으로 partitioning하는 곳에 PIVOT이 위치하는 good split
2. PIVOT이 한 쪽으로 치우친 bad split
   두 가지 split이 가능하다.
   (왜 Q.S.에 randomized behavior를 추가하는지는 Randomized Quick Sort를 설명할 때 설명하도록 하겠다.)

가정: 확률론적으로, 원소들에 대한 모든 순열은 동일하게 일어날 것이다.
따라서, 매 level마다 동일한 방식으로 partitioning이 일어날 것이라고 매우 낮게 예측하며, 그럴 가능성이 없다고 볼 수 있다.
어떤 상황에서는 4-6 partitioning이, 어떤 상황에서는 9-1 partitioning이 일어나고,
항상 best-case나 worst-case partitioning이 일어날 수 없다.
즉, avg-case에서 Partition은 good/bad split을 만들 수 있고, good/bad split은 recursion tree 전반에 랜덤하게 분포된다.

worst-case 예제 Case 1 - 내림차순 정렬된 배열
=> $\Theta(n^2)$

worst-case 예제 Case 2 - 모든 원소가 동일한 값으로 된 배열
=> $\Theta(n^2)$

Improving Quick Sort: Randomized Quick Sort & Tail-Recursive Quick Sort

Randomized Quick Sort

Quick sort의 성능은 각 partition(iteration)에서 pivot에 의존한다.
또한, element의 모든 permutation은 동등하게 일어날 것이라고 가정하고, good/bad split이 랜덤으로 균등하게 일어나길 기대한다.

그러나, 위 가정이 현실에서는 어긋나는 경우가 있다.
실제 시스템 상에서는 대부분 정렬된 경우가 많기 때문에 여기서 퀵소트를 적용한다면, worst-case가 자주 등장할 것이다.(당연히 Pivot의 randomness를 가정하지 않고, 왼쪽 또는 오른쪽 끝에 PIVOT을 둘 때이다.)

이를 해결하기 위해 Randomness를 도입한다.
첫 번째나 마지막 element를 PIVOT으로 사용하는 것 대신에, A[p, …, r]로 구성된 subarray에서 임의로 선택한 element를 PIVOT으로 선택한다.
subarray의 (r-p+1) 개의 원소 중 어떤 것이든 동일한 확률로 PIVOT이 될 수 있다.
=> Randomness의 장점은 split이 good/bad split이 잘 균형잡힌 평균적인 확률로 나타날 수 있다는 것이고, 이것이 성능 향상으로 이어질 수 있다는 것이다.
아래는 Randomized quick sort Pseudo-code 예시이다.

RANDOMIZED-PARTITION(A, p, r)
	i = RANDOM(p, r)
	SWAP(A[r], A[i])
	return PARTITION(A, p, r)

RANDOMIZED-QUICKSORT(A, p, r)
	if p < r
		q = RANDOMIZED-PARTITION(A, p, r)
		RANDOMIZED-QUICKSORT(A, p, q-1)
		RANDOMIZED-QUICKSORT(A, q+1, r)

PARTITION(A, p, r)
  x = A[r]
  i = p-1
  for j=p to r-1
    if A[j] <= x
      i = i + 1
      swap(A[j], A[i])
  swap(A[i+1], A[r])
  return i+1

아쉽게도, worst-case Time complexity는 randomness를 적용하더라도 $\Theta(n^2)$를 따른다.
Avg-case Time Complexity를 계산해보자.
퀵소트의 실행 시간은 Partition이 좌우하기 때문에, 아래와 같은 식으로 평균 시간 복잡도를 작성해볼 수 있다.
(Partition 프로시저가 호출되는 횟수) * cost
cost는 pivot 선택하는데 $\Theta(1)$ + PARTITION 함수 내의 비교 횟수만큼과 동일하다.

그러면, PARTITION 프로시저가 얼마나 많이 호출되는지 알아야 하는데, 잘 생각해보면 한번 pivot으로 선택되면 다시는

Median-of-3 Method

Median as a Pivot 각 subarray의 median 값은 PIVOT이 되기에 가장 적합하다. (=항상 balanced partitioning이 가능하기 때문)
하지만, subarray 내의 median 값을 구하기엔 subarray 전체를 스캔해야 하기 때문에 시간 복잡도 증가
그래서 일반적으로, subarray 내에서 3개의 값을 임의로 골라서, 그 중 median 값을 PIVOT으로 결정할 수 있다. 그러면 좀더 balanced partitioning이 가능하다.

Tail-Recursive Quick Sort

Recursive 알고리즘 (재귀 알고리즘)이란 subproblem들에 대해서 알고리즘 자체를 재귀적으로 호출하는 알고리즘으로, 현재 설명하는 퀵소트와 같은 Divide & Conquer 알고리즘에서는 재귀 구조가 필수적이다.
하지만, 이러한 재귀 구조는 메모리 상에서 스택 오버플로우를 일으킬 수 있다. 이에 대한 해결책으로 사용하는 것이 Tail-Recursive Algorithm이다.

함수에 의해 실행된 마지막 statement가 recursive call 이어야 한다.
즉, recursion 호출을 한 뒤, 메모리 상에 남는 게 없어야 한다.
function call을 stack에 쌓아두지 않는 것이다.
자기 자신만 stack 상에 남아야 한다.

이해가 어려우니 팩토리얼 예제로 예시를 들면,

def factorial(n):
    if n == 1:
      return n
    else:
      return n * factorial(n-1)

위에는 그냥 재귀적인데,

def tail_factorial(n, a):
  if n==1:
    return a
  else:
    return tail_factorial(n-1, n*a)

이번 코드로 다음 factorial 함수 결과를 기다리는 변수 n에 대한 값은 존재하지 않고, 오로지 tail_factorial 함수의 반환값만 스택 프레임에 저장한다.
쉽게 이해하자면, 함수를 종료하기 위해 함수의 마지막에서 함수를 호출하는 방식이다.

위 과정을 퀵소트에도 적용해본다면 다음과 같다.

TAIL-RECURSIVE-QUICKSORT(A, p, r)
while p < r
  //Partition and sort left subarray
  q = PARTITION(A, p, r)
  TAIL-RECURSIVE-QUICKORT(A, p, q-1)
  p = q+1

위 과정을 자세하게 설명해보면,
while 문을 통해 기존 QUICKSORT 코드의 오른쪽 부분을 재귀로 호출하는 것을 피할 수 있다.
partitioning 후에 왼쪽 subarray만 recursive 돌리고, 배열 인덱스 수정후, 다른 subarray에서 반복문으로 처리한다.

Auxiliary Space(보조 공간)이 필요한데, 만약 best-case (균형잡힌 partitioning)라면 $\Theta(\lg n)$의 공간이 필요하지만, worst-case (1:1:1: …)라면, $\Theta(n)$의 공간이 필요하기에 스택 오버플로우가 일어날 수도 있다.
항상 왼쪽만 재귀 호출하면, 재귀 stack-depth가 n에 가깝게 커지기 때문에 stack overflow가 해결되지 않는다. 즉, worst-case의 경우에 stack-depth가 줄지 않는 문제가 발생하므로 어떻게 하면 줄일지 고민해봐야 한다.

해결방법
항상 작은 쪽 부분 배열만 Recursion 돌리고, 큰 쪽 배열은 iterative control structure (반복문)을 이용해 해결하면 된다.
이 경우, stack-depth는 아무리 커져도 $\Theta(\lg n)$ 이다.

QUICKSORT''(A, p, r)
  while p<r
    q <- PARTITION(A, p, r)
    if q-p < r-q
      then QUICKSORT''(A, p, q-1)
        p <- q+1
      else QUICKSORT''(A, q+1, r)
        r <- q-1