[Algorithm] 04. Heap Sort

Heap Data Structure

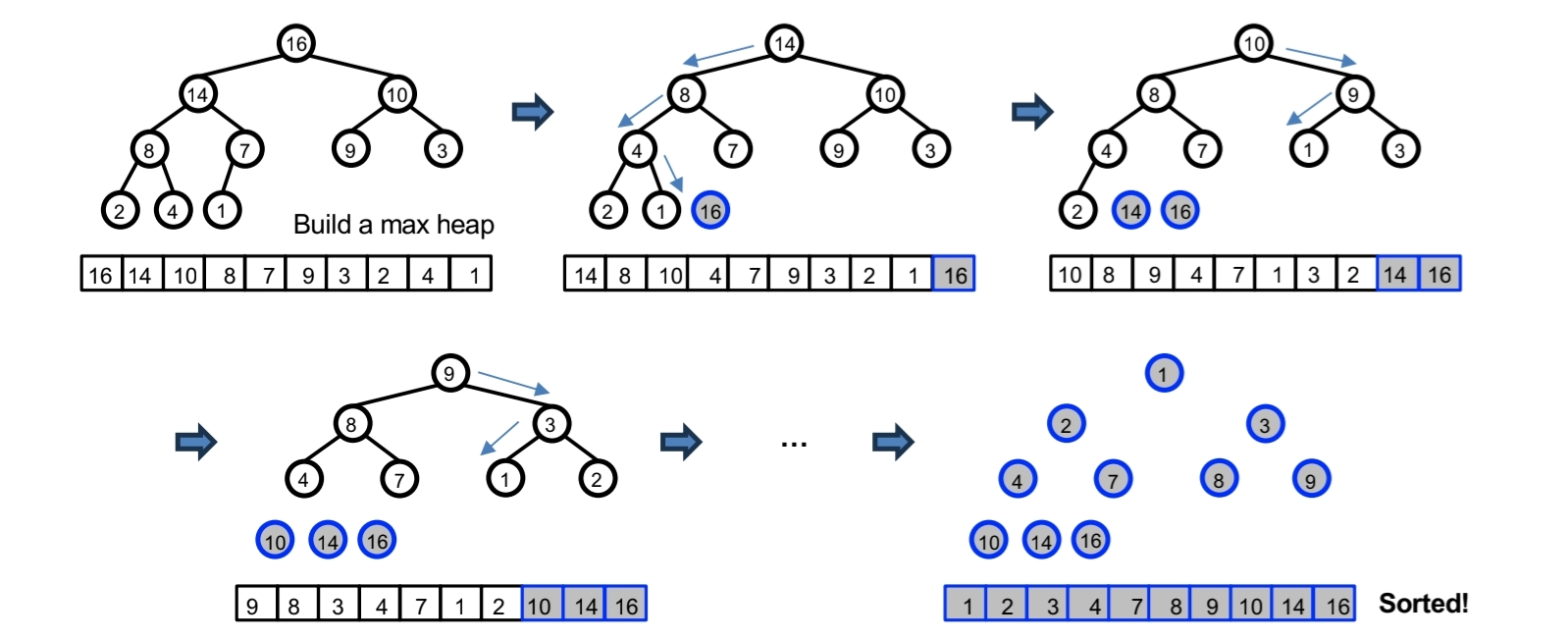
Heap Sort 란?

heap이라는 특수한 자료 구조를 활용하여 정보를 관리하는 정렬 알고리즘

다음과 같은 과정을 통해 heap sort가 진행된다.

1. Max(Min)-heap을 생성
2. 가장 큰(가장 작은) 원소를 heap에서 추출
3. heap 특성을 유지하도록 조정

Heap

Complete Binary Tree의 일종으로 아래의 Heap Property를 만족시켜야 한다.

Heap Property

1. Max-heap property: 부모노드의 key값이 자식노드의 key 값보다 크거나 같은 성질
   $A[Parent(i)] \geq A[i]$
2. Min-heap property: 부모노드의 key값이 자식노드의 key 값보다 크거나 같은 성질

Heap은 배열로 구현한다.

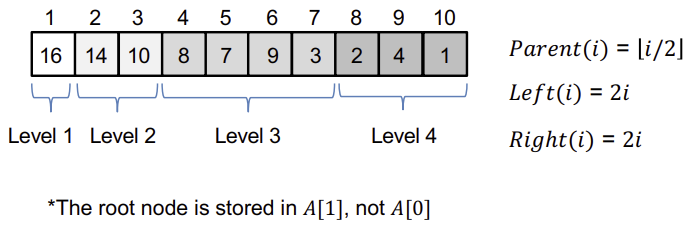
root 노드는 A[1]에 저장된다.
부모 노드의 인덱스는 나누기 2한 인덱스, 왼쪽 자식은 인덱스의 2배, 오른쪽은 2배에 +1한 인덱스이다.

높이가 h인 heap의 노드 개수
마지막 레벨의 노드가 모두 차면 최대이고, 1개만 있으면 최소이다. 결과는 아래와 같다.

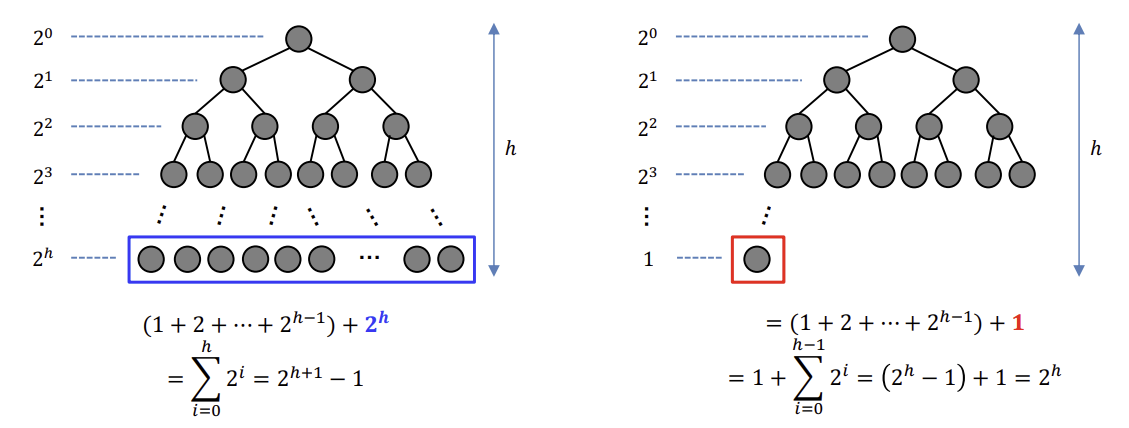
노드 개수를 구했으니, 높이 h에 대한 추정을 할 수 있다.
\(2^h \leq n \leq 2^{h+1} - 1\)
\(2^h \leq n < 2^{h+1}\) 이므로,
\(h \leq \lg n < h+1\)
따라서, $h=\lfloor \lg n \rfloor$ (소수부분을 버린다.)

Heap 생성 방법

1. Max-Heapify
   Heap Property를 유지하기 위해 필요한 함수
   Floating down the value at A[i] in the max heap (= heap 속성을 위반하는, 즉, 자식노드보다 작은 노드인 A[i]를 아래로 이동시키는 과정)
   1) A[i]를 max-heapify 할 것이고, 이것은 subtree의 root 노드이다. max-heap property를 위반한다.
   2) LEFT나 RIGHT 즉, 자기 노드 기준으로 자식 노드에서 A[i]보다 큰 값을 찾는다.
   3) A[i]를 위에서 찾은 큰 값을 가진 자식 노드와 swap한다. 그리고, 자식 노드에서도 동일하게 heap 속성을 만족시킬 수 있도록 recursion 한다.

     MAX-HEAPIFY(A, i)  
      l = LEFT(i)
      r = RIGHT(i)
      if l <= A.heap-size and A[l] > A[i]
        largest = l
      else largest = i
      if r <= A.heap-size and A[r] > A[leargest]
        largest = r
      if largest != i
        swap(A[i], A[largest])
        MAX-HEAPIFY(A, largest)
   

   Max-heapify 함수의 시간복잡도는 처음으로 MAX-HEAPIFY가 적용된 subtree의 높이에 의존한다.
   \(T(n) = \Theta(1) * O(h) = O(\lg n)\)
   여기서, \Theta(1)은 Max-heapify 호출하는데 사용되는 비용이며,
   O(h)는 subtree의 높이이다. worst-case인 root부터 heapify가 시작했을 때, $\lg n$을 따르기 때문이다.
   만약, Max-Heapfity(A, i)가 i > A.heap-size / 2 인 인덱스에서만 일어난다고 하면, 어떤 결과가 나올까?
   아무 일도 일어나지 않는다. A.heap-size/2 인 인덱스는 모두 leaf node 이기 때문에, subtree가 존재하지 않는다. 이미 unit-size subtree이기 때문에 아무리 heapify 호출해도 의미가 없다.
   즉, max-heapify는 internal node에서 의미가 있다.

2. Build-Max-Heap
   배열 A[1 .. n]을 max-heap으로 변환해주는 함수이다.
   MAX-HEAPIFY를 bottom-up 방식으로 사용함으로써 구현한다.
   앞서 언급했다시피, leaf node는 max-heapify가 무의미하므로, $\left\lfloor A.length/2 \right\rfloor$ 값을 가지는 인덱스부터 1번째 인덱스까지 max-heapify를 수행해준다.
   마지막 Internal node부터 시작한다는 의미이다.

     BUILD-MAX-HEAP(A)  
      A.heap-size = A.length
      for i = |A.length/2| downto 1 #LaTeX 수식 표현의 한계로 절대값으로 표현
        MAX-HEAPIFY(A, i)
   

   언제든지 어떤 노드에 Max-heapify가 호출되면, 해당 노드의 subtree는 모두 max-heap이다.
   인덱스 1부터 시작하지 않는 이유는 max-heap property가 유지되지 않기 때문이다.
   BUILD-MAX-HEAP 함수는 for i = |A.length/2| downto 1가 $\Theta(n)$, MAX-HEAPIFY가 $O(\lg n)$를 따르므로, $O(n \lg n)$의 시간복잡도를 갖는다고 말할 수 있다. 하지만, 점근적으로 tight한 bound를 가진다고 말하기는 힘들다. 대부분의 subtree의 높이는 $\lg n$보다 작기 때문이다.
   좀 더 tight한 bound를 잡기 위해서 다음과 같은 식을 통해서 시간 복잡도를 계산해보자.
   (높이를 h로 갖는 원소의 개수) * (높이 h)
   그렇다면 높이 h를 가지는 원소의 개수에 대한 수식이 필요하다.
   결론부터 내리면, 높이 h를 가지는 노드는 최대 $\lceil \frac{n}{2^{h+1}} \rceil$ 개 존재한다.
   자세한 증명은, 직접 노드 개수와 높이 h를 가지고 쉽게 유도할 수 있으니 생략한다.
   이제부턴 수학공식들을 활용해 시간복잡도를 도출해낼 것이다.
   \(\sum_{h=0}^{\lfloor \lg n \rfloor} \lceil \frac{n}{2^{h+1}} \rceil O(h) = O(n\sum_{h=0}^{\lfloor \lg n \rfloor} \frac{h}{2^h})\)
   \(\sum_{h=0}^{\lfloor \lg n \rfloor} \frac{h}{2^h}\) 이 식에서 $\lg n$ 대신 무한대를 넣어서 무한급수를 만들면, 무한급수 공식을 미분하고 다시 공비를 곱하는 과정을 통해서 특정 상수 값에 수렴하는 공식이 하나 나온다. (이 과정은 생략.)
   즉, $\sum_{h=0}^{\infty} \frac{h}{2^h}$가 특정 상수, 정확히는 2에 수렴하므로, 최종적인 BUILD-MAX-HEAP의 시간복잡도의 aymptotic-tight-upper-bound는 $O(n)$임을 알 수 있다.
   즉, build-max-heap은 선형 시간을 가진다.

Heap Sort

1. Build-Max-Heap
2. 가장 큰 값이 된 A[1]인 root 노드의 원소를 추출한다. 배열 A 상 마지막 인덱스의 노드(정확히는 element. 원소.)와 swap해서 기존 heap 배열의 적절한 위치에 추가한다.
3. MAX-HEAPIFY(A, 1)을 호출해서 heap property를 만족시키도록 한다. 자연스럽게 그 다음 큰 원소가 root 노드에 위치하게 된다.(=A[1]에 위치)

HEAPSORT(A)
  BUILD-MAX-HEAP(A)
  for i=A.length downto 2
    swap(A[1], A[i])
    A.heap-size = A.heap-size - 1
    MAX-HEAPIFY(A, 1)

heap에서 leaf node에 위치하는 원소들부터 차근차근 sorting해서 전체를 정렬한다.

Heap Sort: Performance

Heap Sort의 시간복잡도: \(O(n \lg n)\)
BUILD-MAX-HEAP이 $O(n)$을 만족하고, MAX-HEAPIFY와 함께 loop 도는 게 $O(n) * O(\lg n)$이라 더하면 위와 같이 나온다.
Heap Sort의 공간복잡도: \(\Theta(1)\)
in-place 정렬로, 기존 heap 공간에서 정렬될 수 있다.
추가적인 공간이 필요없다.

굳이 마지막 노드와 root 노드를 swap하는 이유는, heap property도 만족 안 하기 때문이고, 빈 공간으로 마지막 노드를 옮기지 않는 이유는 complete binary tree 속성을 잃기 때문이다. (heap이 더이상 아님)
즉, complete binary tree이면서 max-heap property를 만족하고, in-place sorting 하기 위해서 root 노드를 마지막 노드와 swap하는 것이다.

cf. heap에서 search 함수는 전체 배열을 다 훑어야 한다.

Priority Queue

우선순위에 기반해 큐 내의 원소를 배치하는 자료구조이다.
우선순위가 높은 원소들이 먼저 retrieve(검색) 된다.
만약 priority를 순서에 두고 있다면, Queue와 동일하다.

우선순위 큐는 CPU 스케줄링, Huffman coding algorithm, 다익스트라 알고리즈, Prim 알고리즘 등에 사용된다.

우선순위 큐는 heap을 통해 구현되고, Get Maximum, Extract Maximum 함수와 핵심이 되는 Increase Key와 Insertion 함수에 대해서 살펴본다.

Get Maximum

$O(1)$의 시간복잡도를 가지며, 가장 우선순위가 높은 원소를 검색한다.

HEAP-MAXIMUM(A)
  return A[1]

Extract Maximum (=deletion)

$O(\lg n)$의 시간복잡도를 가지며, 가장 우선순위가 높은 원소를 추출해내고, Max-heapify를 통해 우선순위 큐를 재조직한다.

HEAP-EXTRACT-MAX(A)
  if A.heap-size < 1
    error "heap underflow"
  max = A[1]
  A[1] = A[A.heap-size]
  A.heap-size = A.heap-size - 1
  MAX-HEAPIFY(A, 1)
  return max

Increase Key

$O(\lg n)$의 시간복잡도를 가진다.
특정 원소의 priority를 증가시키고 싶을 수도 있다. 그때 사용하는 함수이며, key가 priority를 나타내기 때문에, 현재 key보다 큰 값을 priority로 바꿔야 한다.(무조건)
그리고, 우선순위를 증가시키는 것은 heap property를 위반하기 때문에, 부모 노드랑 계속 비교하고 swap하면서 heap property를 만족시키도록 코드를 작성해야 한다.

HEAP-INCREASE-KEY(A, i, key)
  if key < A[i]
    error "new key is smaller than current key"
  A[i] = key
  while i > 1 and A[PARENT(i)] < A[i]
    swap(A[i], A[PARENT(i)])
    i = PARENT(i)

Insertion

새로운 원소를 우선순위 큐에 삽입할 때 사용하는 함수이다. 시간복잡도는 $O(\lg n)$
새로운 원소를 마지막 leaf node에 삽입하고, INCREASE-KEY를 호출해 max-heap property를 유지하도록 한다.

MAX-HEAP-INSERT(A, key)
  A.heap-size = A.heap-size + 1
  A[A.heap-size] = -∞
  HEAP-INCREASE-KEY(A, A.size, key)