[Algorithm] 06. Dynamic Programming (1)
Introduction to Dynamic Programming
Subproblem에 대한 Solution을 결합함으로써 복잡한 문제를 풀어나가는 것
D&Q vs DP
- D&Q(Divide & Conquer)
subproblem이 독립적임
subproblem에 대한 solution이 공유되지 않음!! - DP(Dynamic Programming)
subproblem이 독립적이지 않음
subproblem을 오로지 한번만 해결하고, solution을 저장해서 재사용함
-> 불필요한 연산 피함(avoid redundant computations)
Example of DP: Computing n-th Fibonacci Number
$\mathrm{Fibo}[n] = \mathrm{Fibo}[n-1] + \mathrm{Fibo}[n-2]$
e.g. 0, 1, 1, 2, 3, 5, 8, …
- D&Q 구현
1 2 3 4
def fibo_recursion(n): if n <= 1: # base case return n return fibo_recursion(n-1) + fibo_recursion(n-2)
Time Complexity: $T(n) = T(n-1) + T(n-2) + 1$, 결국 $O(2^n)$
각 함수가 재귀적으로 다른 두 함수를 호출하는 형태
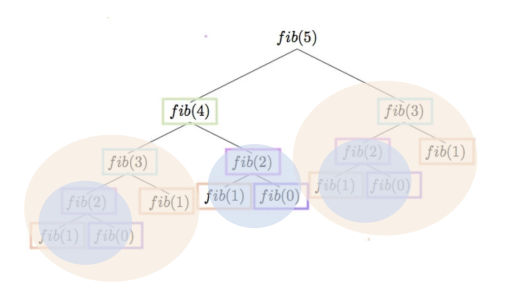
위 그림과 같이 중복되는 불필요한 subproblem들이 너무 많다. - DP - Memoization
1 2 3 4 5 6 7 8 9 10
def fibo_memoization(n, cache): if n in cache: return cache[n] if n <=1: cache[n] = n else: cache[n] = fibo_memoization(n-1, cache) + fibo_memoization(n-2, cache) return cache[n]
원래 problem을 재귀적으로 subproblem으로 쪼개면서 해결해 나가는 부분은 동일하다.
하지만, cache라는 배열에 subproblem의 solution을 저장한다.
만약 solution이 저장된 게 있으면, 즉, 동일한 subproblem을 맞닥뜨렸을 때 그 값을 재사용한다.
그래서, 각 subproblem은한번만수행된다.
Time Complexity: $O(n)$ => 엄청난 시간복잡도 감소를 만든다.
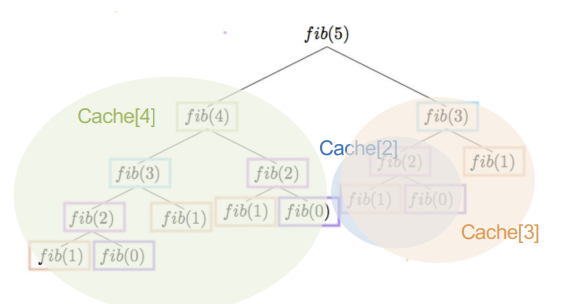위 그림처럼 중복되는 subproblem들은 cache에 저장된 값으로 처리한다.
Goal of Dynamic Programming
DP는 최적화 문제에 적용한다.
아래 예시를 간략하게 소개하며, 후술할 예정이다.
예1) 막대기를 여러 개로 자르고 팔게 되면서 생기는 이익을 최대화하는 문제(막대기를 몇 개로, 얼마의 길이로 자르면 수익이 최대가 되는지)
예2) 행렬의 곱연산에서 연산 비용을 최소화하는 문제(어느 행렬부터 연산해야 가장 적게 연산하는지)
최적화 문제에 정답은 많지만, 그 중에서도 Maximum/Minimum인 최적의 값을 구하는 것이 목표이다.
최적화 문제의 solution은 한 가지가 아니기에 the optimal solution이 아닌 an optimal solution이라 부른다. (예를 들어, 막대기 수익을 최대화하는 커팅 방법이 2~3개 있을 때, 우리는 어쨌든 그 중 하나만 구하면 되기 때문에)
Applying Dynamic Programming
- 최적해의 구조적 특성을 파악하기
= 전체 문제의 최적해가 부분 문제의 최적해로 어떻게 이뤄지는지 파악하기 - 최적해의 값을 재귀적으로 구하기
= 부분 문제를 기반으로 전체 문제의 최적해의 값을 재귀적으로 계산할 수 있는 관계식 세우기 - 각 부분 문제(subproblem)에 대한 최적해의 값을 계산하고 저장하기(중복 계산 피하기)
- Top-down (Memoization)
- Bottom-up (Tabulation)
- 계산된 정보(=저장된 최적해의 값들)로부터 원래 문제에 대한 최적해를 구하기
- Top-down => 메모이제이션 된 값들을 따라가면서 최적해 재구성 (=traceback)
- Bottom-up => 테이블을 채워나가면서 마지막 cell에 최적해 도달
=> 각 subproblem은 오직 한번만!!!
Rod Cutting Problem
Problem Definition & Optimal Solution
길이가 n인 막대와 $i = 1,2,3,\cdots,n$에 대한 가격 $p_i$의 표가 주어지면 해당 막대를 잘라서 판매했을떄 얻을 수 있는 최대수익 $r_n$을 결정하는 것
(길이가 n인 막대의 가격 $p_n$이 충분히 비싸면 최적해는 자르지 않은 것일 수도 있음)
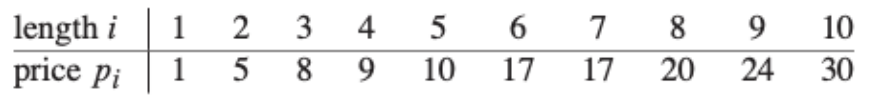
막대 길이가 n일 때, 자르는 경우의 수는 $2^{n-1}$가지가 존재하므로, naive한 방식으로 해결하려 한다면, 저 경우의 수를 전부 비교해 $O(2^n)$의 시간복잡도를 가진다. 너무 오래 걸린다.
간단한 예시를 들어보자. 만약 4-inchj 막대기가 있다면, $2^3=8$가지의 경우의 수가 존재한다.
4 | 1+3 | 2+2 | 3+1 | 1+1+2 | 1+2+1 | 1+2+1 | 1+1+1+1 |
위 표를 통해서 최적해를 찾아보면, (2+2)일 때, 10달러로 최적해를 도출함을 알 수 있다.
Optimal Solution을 조금 더 일반화해보면,
만약 최적해가 k개의 조각으로 잘리는 상황이라고 했을 때($1 \leq k \leq n $),
$n = i_1 + i_2 + \cdots + i_k$
여기서 i는 k번째 막대기의 길이다.
$r_n = p_{i_1} + p_{i_2} + \cdots + p_{i+k}$
최적해를 구할 수 있다.
조금 더 일반화해보면,
\(r_n = max(p_n, r_1+r_{n-1}, r_2+r_{n-2}, \cdots, r_{n-1}+r_1)\)
$p_n$은 no cut. 즉, 잘리지 않은 상태도 최대 수익이 가능하므로, 별개로 구하고, 나머지는 크기가 각각 $i$와 $n-i$인 두 개의 잘린 막대기의 최대 수익을 구하는 것과 동일하다.
즉, subproblem을 2개의 막대기를 분할함으로써 만들어낸 것이다.
쉽게 생각해보면, 7 = 1 + 1 + 2 + 3 이 될 수 있지만, 2 + 5가 될 수도 있다. 어? 이러면 수익이 달라지는 것 아닌가? 생각할 수 있지만 이미 우리는 막대기 길이가 5인 혹은 2인 막대기의 최대 수익을 알 수 있다고 가정한다. (subproblem으로 나눠서 그 때 계산하면 됨)
즉, 전체 최적해는 2개의 subproblem에서의 최적해를 합쳐서 얻을 수 있고, rod-cutting problem은 optimal substructure를 가진다.
뿐만 아니라, 막대기를 처음에 $i$ 길이로 자르고, 나머지 길이 $n-i$가 생기는데 이것도 같은 방식으로 자를 수 있다. 즉, 길이가 n인 막대기 자르는 문제를 i + (n-i)로 나누고 (n-i) 또한 새로운 subproblem으로 쪼개져 재귀적인 방식으로 최적해를 찾는다.
즉, 전체 자르기(Decomposition)은 처음 자른 조각 + 남은 막대 자르기이고, 간결한 식으로 나타내면,
\(r_n = \displaystyle \max_{1 \leq i \leq n} (p_i + r_{n-i})\)
$p_i$는 first piece고 $r_{n-i}$는 remainder고 여기의 최적해에 집중하면 된다.
Applying dynamic programming
- Naïve Solution(DP X)
1 2 3 4 5 6 7
CUT-ROD(p, n) if n==0 return 0 q = -∞ for i=1 to n q = max(q, p[i]+CUT-ROD(p, n-i)) return q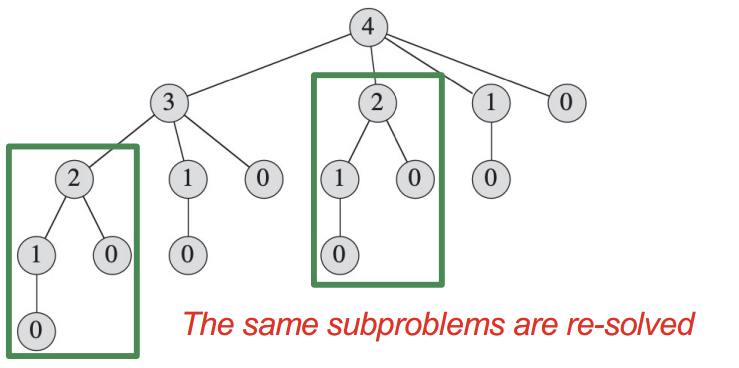
보다시피, 불필요한 연산이 중복되고,
T(0)=1, T(1)=2, T(2)=4, …
$T(n)=2^n$ 길이 n에 대해 exponential한 형태로 시간복잡도를 가지게 된다. - Dynamic Programming
각 subproblem이 한번만 풀어지게 arrange하고, 각각의 subproblem에 대한 해를 테이블에 저장하며, 나중에 그 해가 필요할 때 테이블을 보고서 필요한 값을 사용한다.
Time Complexity가 $O(2^n)$ -> $O(n)$이 되는 대신에, 그만큼 추가적인 메모리가 필요하다.- Memoization
각 subproblem의 해를 저장하고, 이미 풀었던 subproblem에 대한 solution 값이 있으면 그 값을 불러와 사용한다.1 2 3 4 5
MEMOIZED-CUT-ROD(p, n) let r[0 .. n] be a new array # For memo for i=0 to n r[i] = -∞ return MEMOIZED-CUT-ROD-AUX(p, n, r) # Top, 즉, main problem인 n부터 시작한다.1 2 3 4 5 6 7 8 9 10
MEMOIZED-CUT-ROD-AUX(p, n, r) if r[n] >= 0 # If the optimal revenue for a rod of length n is already computed. return r[n] if n == 0 q = 0 else q = -∞ # 없으면 값을 계산하고 r(=cache) 배열에 결과를 저장한다. for i=1 to n q = max(q, p[i]+MEMOIZED-CUT-ROD-AUX(p, n-i, r)) r[n] = q return qTime Complexity: $\Theta(n^2)$
- Tabulation
가장 작은 subproblem부터 시작해, 크기 순으로 해결해나간다.
특정 subproblem을 풀 때, 더 작은 subproblem에서 이미 구했던 해를 사용해 시간을 줄인다.
size에 대해 subproblem들을 정렬하고, 가장 작은 subproblem부터 크기 순으로 문제를 해결해나간다.1 2 3 4 5 6 7 8 9
BOTTOM-UP-CUT-ROD(p, n) let r[0 .. n] be a new array # For table r[0] = 0 for j=1 to n # Start from bottom q = -∞ for i=1 to j q = max(q, p[i]+r[j-i]) # r[j-i]는 이미 계산된 값! r[j] = q return r[n]Time Complexity: $\Theta(n^2)$
- Memoization
Understanding of DP Problems
DP 문제를 해결하기 위한 key point는
- problem과 관련된 개별 subproblem의 집합을 이해
- subproblem이 다른 subproblem들에 어떻게 의존하는지 이해
위 2가지이다.
Subproblem Graph
위 2가지 key point를 담은 directed graph이다.
G(V, E)로 나타내며 위에서 언급한 1번은 Vertex로, 2번은 Edge로서 표현된다.
더 자세히 설명하자면,
Vertex: 각각 개별의 subproblem을 나타내고, 그것의 크기를 labeling 한다.
Edge(x, y): subproblem x를 풀기 위해 subproblem y의 해가 필요한 상황, 의존 관계 표현. 즉, 이 사실을 통해 Memoization이든 Tabulation이든 문제를 푸는 방향과 상관없이 그냥 의존 관계에 의해 Edge를 표현함을 알 수 있음.
정리하자면,
개별 subproblem의 총 개수는 Vertices의 개수와 같고, subproblem에 대한 해를 계산하는 총 비용은 vertex의 degree와 같다.
따라서, DP의 실행 시간은 vertices 및 edges의 개수와 linear한 관계에 있음을 알 수 있다.
Reconstructing a Solution
눈치를 챘을 수도 있지만, 위 pseudocode는 r[n]이나 q 즉, 최적해의 값만을 반환하기 때문에, 우리가 원하는 decomposition에 대한 대답은 못한다. 어떤 길이의 조합이 필요한지를 return하지 못하는 것이다.
우리는 어느 위치에서 막대기를 잘라야 하는지를 알아야 한다.
각 subproblem에 대한 최적해 뿐만 아니라, 최적해를 이끄는 choice 또한 알아야 한다.
우선, 위에서 언급했던 Tabulation 기반의 pseudocode 바탕으로 살펴보면, 아래와 같이 리팩토링 가능하다.
1
2
3
4
5
6
7
8
9
10
11
EXTENDED-BOTTOM-UP-CUT-ROD(p, n)
let r[0 .. n] and s[0 .. n] be new arrays
r[0] = 0
for j=1 to n
q = -∞
for i=1 to j
if q < p[i] + r[j-i]
q = p[i] + r[j-i]
s[j] = i
r[j] = q
return r and s
추가적으로, Memoization 방법도 아래와 같이 r, s를 도출하도록 바꿀 수 있다.
1
2
3
4
5
6
EXTENDED-MEMOIZED-CUT-ROD(p, n)
let r[0 .. n] and s[0 .. n] be new arrays
for i=0 to n
r[i] = -∞
EXT-MEMOIZED-CUT-ROD-AUX(p, n, r, s)
return r and s
1
2
3
4
5
6
7
8
9
10
11
12
13
EXT-MEMOIZED-CUT-ROD-AUX(p, n, r, s)
if r[n] >= 0
return r[n]
if n == 0
q = 0
else q = -∞
for i=1 to n
temp = p[i] + EXT-MEMOIZED-CUT-ROD-AUX(p, n-i, r, s)
if q < temp
q = temp
s[n] = i
r[n] = q
return q
Tabulation이나 Memoization 모두 아래와 같은 수도코드를 통해, 각 길이에서의 최대 비용과 cutting 하는 위치(=길이)를 알 수 있다.
즉, 아래와 같은 표를 얻을 수 있다.
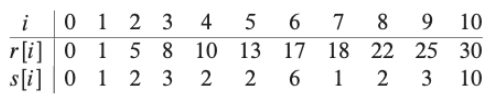
1
2
3
4
5
PRINT-CUT-ROD-SOLUTION(p, n)
(r, s) = EXTENDED-MEMOIZED-CUT-ROD(p, n)
while n > 0
print s[n]
n = n - s[n]
Implementation an O(n)-time dynamic-programming alogirhtm for Computing the n-th Fibonacci Number
1
2
3
4
5
6
7
8
9
10
11
def fibo_tabulation(n):
table = [0] * (n+1)
table[1] = 1
if n <= 1:
return table[n]
for i in range(2, n+1):
table[i] = table[i-1] + table[i-2]
return table[n]
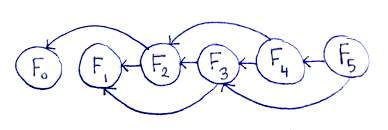
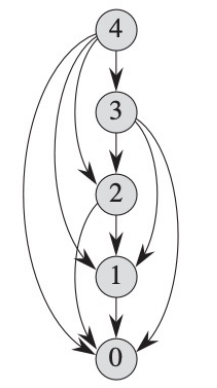
위 그림에서 유추할 수 있듯이,
Vertices: (n+1) 개, Edges: (2n-2) 개이다.
Matrix-Chain Multiplication Problem
Problem Definition & Optimal Solution
컴퓨팅 리스소는 제한되기 때문에, 행렬곱연산을 가장 효율적으로 하는 순서를 알아내고 싶은 상황이다.
즉, computational cost를 최소화하는 행렬곱연산 방식을 구하는 것이 목표이고, 최적화 문제이다.
Characteristic of Matrix Multiplication
Compatibility
두 행렬의 연산가능성에 대한 설명으로, A와 B 행렬이 있을 때, A 행렬의 열의 개수가 B 행렬의 행 개수와 동일해야 Compatible하다고 판단한다.
AB의 연산결과인 행렬 C는 A(pxq), B(qxr)이라고 했을 때, pxr의 형태로 나타난다.
행렬 곱의 computational cost는 스칼라 곱의 개수에 의해 결정된다.
이게 뭔소리냐면,
A(pxq) X B(qxr) = C(pxr) 과 같은 행렬곱이 있을 때,
pqr회의 연산이 필요하다는 것이다.
1
2
3
4
5
6
7
8
9
10
MATRIX-MULTIPLY(A, B)
if A.columns != B.rows
error "incompatible dimensions"
else let C be a new A.rows X B.columns matrix
for i=1 to A.rows
for j=1 to B.columns
$c_ij$ = 0
for k=1 to A.columns
$c_ij$ = $c_ij$ + $a_ik$ * $b_kj$
return C
하지만, 행렬곱은 결합법칙이 성립하고, 곱셈 순서를 바꿀 수 있는데, 이때 연산의 양인 pqr이 달라질 수 있다.
Parenthesization이라고 말하며, 행렬들에 괄호를 쳐서 먼저 수행될 행렬곱을 결정하는 과정이라고 해석하면 좋을 것 같다.
간단한 예제로, 문제 상황을 이해해보자.
$A_1$: 10 x 100, $A_2$: 100 x 5, $A_3$: 5 x 50 과 같이 행렬이 존재한다고 했을 때, 두 가지 경우의 수가 있다.
- $(A_1 \cdot A_2) \cdot A_3$
1번의 경우, (10 * 100 * 5) + (10 * 5 * 50) = 5000 + 2500 = 7500 회의 연산이 필요하다. - $A_1 \cdot (A_2 \cdot A_3)$
2번의 경우, (100 * 5 * 50) + (10 * 100 * 50) = 25000 + 50000 = 75000 회의 연산이 필요하다.
즉, 뒤에서부터 행렬곱하는 간단한 과정(Parenthesization)을 통해서 10배 더 빠른 연산이 가능하다는 것이다.
따라서, 다시 문제를 정리하면, 실제 행렬곱을 하는 것은 아니며, 가장 적은 비용으로 가장 최고의 parenthesization을 하는 것이 목표이다.
Given a chain $<A_1, A_2, \cdots, A_n>$ matrices, to fully parenthesize the product $A_1A_2 \dots A_n$ in a way that minimizes the computational cost.
Naïve Approach
일일이 다 해보고 비교하는 brute-force 방식이다.
- 가능한 모든 parenthesization을 나열
- 각 parenthesization의 스칼라곱의 횟수를 계산한다.
- 스칼라곱 연산이 최저인 parenthesization 방식을 선택한다.
증명은 생략하고, rod-cutting과 비슷하게 $\Omega(2^n)$의 시간복잡도를 가진다.
Solution to Matrix-Chain Multiplication using DP
- 최적해의 구조적 특성을 파악하기
= 전체 문제의 최적해가 부분 문제의 최적해로 어떻게 이뤄지는지 파악하기 - 최적해의 값을 재귀적으로 구하기
= 부분 문제를 기반으로 전체 문제의 최적해의 값을 재귀적으로 계산할 수 있는 관계식 세우기 - 각 부분 문제(subproblem)에 대한 최적해의 값을 계산하고 저장하기(중복 계산 피하기)
- Top-down (Memoization)
- Bottom-up (Tabulation)
- 계산된 정보(=저장된 최적해의 값들)로부터 원래 문제에 대한 최적해를 구하기
- Top-down => 메모이제이션 된 값들을 따라가면서 최적해 재구성 (=traceback)
- Bottom-up => 테이블을 채워나가면서 마지막 cell에 최적해 도달
최적해의 구조적 특성 파악
rod-cutting과 동일한 방식으로 해결해나간다고 생각하면 쉽다.(2개의 subproblem을 처리하는 형식으로 문제를 쪼갠다.)
$A_{i..j}$를 $A_iA_{i+1} \cdots A_j$에 대한 행렬곱을 연산한 결과 행렬이라고 가정할 때,
$A_{i..j} \quad (i \leq k < j)$ 의 연산 비용은 $((A_iA_{i+1} \cdots A_k)(A_{k+1}A_{k+2} \cdots A_j))$ 에서
Total cost: ($A_{i..k}$의 연산비용) + ($A_{k+1..j}$의 연산비용) + ($A_{i..k}$와 $A_{k+1..j}$를 곱하는데 사용되는 비용)
이라고 정리할 수 있다.
즉, 최적의 parenthesization을 가지는 두 개의 subchain을 parenthesize하는 것은 최적해를 만든다.- 최적해의 값을 재귀적으로 구하기
$m[i, j]$를 $A_iA_{i+1} \cdots A_j$ 계산하는 최소 비용이라고 할 때,
다음과 같은 수식 수립이 가능하다.
\(m[i, j] = m[i, k] + m[k+1, j] + p_{i-1}p_kp_j\)
여기서 $p_{i-1}$은 왼쪽 행렬의 행수, $p_j$는 오른쪽 행렬의 열수
$p_k$는 정확하게 모르기 때문에 실제로 $i \leq k < j$ 범위 내에서 모든 가능한 k를 찾아 최적의 비용을 찾아내야 한다.
아래는 Bottom-up 방식으로 구현한 Pseudocode이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
MATRIX-CHAIN-ORDER(p)
n = p.length - 1
let m[1..n, 1..n] and s[1..n-1, 2..n] be new tables //subproblem에 대한 solution을 저장하기 위한 2차원 배열을 2개 생성한다.
for i=1 to n
m[i, i] = 0
for l=2 to n // l은 chain의 길이를 의미한다.
for i=1 to n-l+1 // sliding window (window size = l)
j = i+l-1
m[i, j] = ∞
for k=i to j-1 // $A_{i..j}$를 연산하는데 필요한 최소 비용을 찾는다.
q = m[i, k] + m[k+1, j] + $p_{i-1}p_kp_j$
if q < m[i,j]
m[i, j] = q
s[i, j] = k // 최적해를 reconstructing하기 위해 최적해 k 값을 저장한다.
return m and s
Example of Matrix-Chain Multiplication
Given a sequence $<A_1, A_2, A_3, A_4, A_5, A_6>$, compute the minimum cost of computing the product $A_1A_2A_3A_4A_5A_6(m[1,6])$
Complexity of Tabulation Approach
Time Complexity: $O(n^3)$
subproblem의 총 개수: $O(n^2)$ 각 subproblem에서의 시간: $O(n)$
Space Complexity: $O(n^2)$
m, s table 보면 알 수 있음
Element of DP
Optimal Substructure
문제에 대한 최적해가 subproblem에 대한 최적해로 구성되어 있을 때 Optimal substructure를 가진다고 표현한다.
논의 사항
항상 optimal substructure가 있다고 단정하면 안 된다.
특히, 그래프 문제에서 성립하지 않을 가능성이 있다.
Problem 1) Unweighted shortest path (정점 u에서 v까지 가장 적은 edge로 가는 경로 찾기)
cycle이 없는 simple path인 상황이어야 한다. optimal substructure가 성립한다고 말할 수 있는데, 그 이유는 아래와 같다.
u에서 v까지 가는 가장 짧은 경로가 만약 w라는 정점을 포함한다면,
u에서 w까지 경로 또한 최단 경로이고, w에서 v까지의 경로도 최단 경로이기에 optimal structure가 성립한다고 볼 수 있음
Problem 2) Unweighted longest simple path (정점 u에서 v까지 가장 많은 edge 수를 가지는 simple path 찾기)
결론부터 말하면, optimal substructure가 성립하지 않는데, u에서 v까지의 최장 단순 경로가 w를 무조건 지난다고 하면,
u에서 w로 가는 가장 먼 단순 경로가 u->w는 아니기 때문이다.
예를 들어서, (q,s,r,t가 상호 순환하는 그래프 모양이라고 가정하면) q->t 인 longest simple path는 q->r->t 혹은 q->s->t인데,
q->r에 대한 최장 단순 경로는 q->s->t->r이므로 optimal structure 성립하지 않음
Overlapping Subproblems
재귀 알고리즘이 계속해서 같은 문제를 반복해서 방문할 때를 말한다.
subproblem의 공간은 작아야 한다. 즉, 개별 문제의 총 개수는 작아야 한다.
cf. DP의 실행 시간
다음 두 가지 요인에 의해 결정된다.
- 원래 문제에 대한 최적해가 사용하는 subproblem의 개수
- 각 subproblem를 해결할 때, 얼만큼의 choice를 고려해야 하는지
예를 들면, rod-cutting에서
- $\Theta(n)$개의 subproblem이 존재
- 최대 n개의 choice가 가능
=> 실행시간은 $O(n^2)$
Matrix-chain Multiplication
- $\Theta(n^2)$개의 subproblem이 존재
- 최대 (n-1)개의 choice가 가능
=> 실행시간은 $O(n^3)$