[Algorithm] 07. Greedy Algorithm
매 순간 최선의 선택을 하는 그리디 알고리즘을 다룹니다.
Introduction to Greedy Algorithm
앞선 포스트에서 설명했던, DP는 최적화 문제에 대한 접근법이었다.
해당 문제를 구성하고 있는, subproblem들이 해결된 후에 가장 좋은 방법을 찾는다.
그리디도 best choice를 한다는 점은 비슷하지만 “locally”라는 조건이 붙는다.
Subproblem이 해결되기 전에, locally best choice를 하여 결국 global optimal solution을 얻는 알고리즘
Problem 1: Activity-selection problem
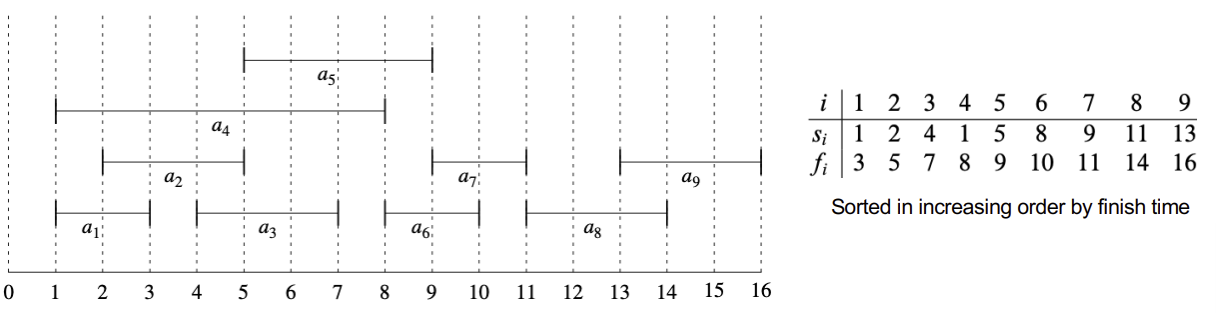
$S=\{a_1, a_2, \cdots, a_n\}$인 집합 S는 자원을 사용하길 바라는 n개의 활동들로 구성되어 있고,
이 문제의 목표는 maximum-size subset of mutually compatible activities(서로 양립 가능한 활동들의 최대 크기 부분 집합)을 고르는 것이다.
각 활동 $a_i$는 시작 시간 $s_i$과 $f_i$로 구서오디어 있고,
$a_i$와 $a_j$가 compatible(양립 가능함)한 것은 각 시작시간과 종료시간의 간격 $[s_i, f_i)$, $[s_j, f_j)$이 겹치지 않는 상황을 말한다.
즉, compatible 한 activity 이면서 동시에 집합의 크기가 최대여야 한다.
Optimal Structure & DP
앞으로, $S_{ij}$를 $a_i$가 끝나고부터, $a_j$가 시작하기 전의 시간 간격에 속하는 활동의 집합으로 정의할 것이다.
예를 들면, 위 그림에서 $S_{4 8}= \{a_6, a_7\}$로 표현할 수 있다.
추가로, $A_{ij}$를 $S_{ij}$에 대한 최적해로 표기할 것이다.
예를 들면, $S_{1 9} = \{a_3, a_5, a_6, a_7 \}$인데,
$A_{1 9} = \{a_3, a_6\} or \{a_3, a_7\} or \{a_5, a_7\}$로 표기할 수 있다.
만약, 최적해인 $A_{ij}$가 $a_k$를 포함하고 있다면,
\(A_{ij} = A_{ik} \cup \\{a_k\\} \cup A_{kj}\)
즉, $S_{ik}$와 $S_{kj}$의 substructure를 통해 문제를 해결할 수 있다.
이걸 DP로 접근하게 되었을 때, 풀어야 하는 subproblem의 개수가 너무 많고, main problem을 해결하는 방법이 효율적이지 않다.
Greedy Approach
- 모든 subproblem을 풀짖 않고 greedy choice(당장 가장 좋은 선택을 하는 것)
그렇다면, Activity-Selection 문제에서는?
매 iteration마다 finish time이 가장 빠른 activity를 선택하는 것
DP처럼 두 개의 subproblem을 풀어야 되는 것이 아닌, 하나만 관리하면 된다.
왜 그런지는 직관적으로 알 수 있다.
가장 빨리 끝나는 활동을 고르면, 여러 최적해 중 하나를 포함할 수 있다.
Pseudo Code
GREEDY-ACTIVITY-SELECTOR(s, f)
n = s.length
A = {a1}
k = 1
for m=2 to n
if s[m] >= f[k] //compatible한지 체크
A = A ∪ {am}
k = m
return A
그리디 방식의 접근은 activity selection problem을 선형 시간에 풀어낸다.
즉, n개의 활동에 대해서 $\Theta(n)$ 시간에 풀어낸다.
(DP는 subproblem 개수 $O(n^2)$, subproblem 선택하는 개수 $O(n)$. 총 $O(n^3)$의 시간이 소요된다.)
(그리디도 정렬이 안 된 상태라면 $O(n \lg n)$의 시간을 더 써야 한다.)
DP vs. Greedy
| DP | Greedy |
|---|---|
| subproblem이 해결된 후에 선택 | subproblem이 해결되기 전에 선택 |
| subproblem 여러 개가 생성됨 | subproblem이 단 한 개 생성됨 |
| 복잡하고 더 느림(구현 및 실행시간) | 단순하고 더 빠름 |
| subproblem에 대한 solution을 재사용함 | subproblem에 대한 solution을 재사용하지 않음 |
| - | main 문제에 대한 최적의 해를 제공하지 못 할 수도 있음 |
Elements of the Greedy Approach
선택하는 그 시점에서 가장 좋은 선택을 함으로써 최적해를 얻는다.
때론 최적해를 도출하지 못할 수도 있지만, 때론 가능함. => 그 기준, 조건이 뭘까?
Greedy-choice property
Global 최적해가 local에서의 최적의 선택을 모아서 만들어진다.
DP처럼 첫번째 선택을 하기 전에 subproblem을 해결하지 않고, subproblem을 해결하기 전에 선택을 하는 것. 당장 best choice를 선택.
그리디에 의한 선택은 지금까지의 선택에 의존하지만, 미래의 선택에는 의존하지 않음.
Optimal Substructure
문제에 대한 최적해는 subproblem에 대한 최적해를 포함함.
Greedy: Knapsack Problem
0-1 Knapsack Problem
도둑이 n 개의 물건을 훔치고, 가능한 비싼 물건들을 가져오고 싶어함.
i번째 item은 $v_i$ 달러, $w_i$ 파운드임.
도둑이 최대 W 파운드를 담을 수 있는 배낭을 가지고 있다고 할 때,
어떤 물건을 가지고 와야 하는지?
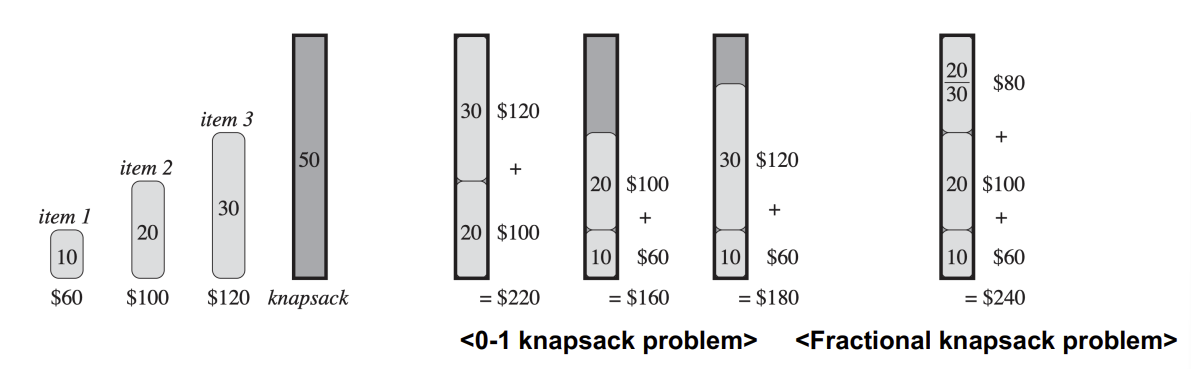
0-1 Knapsack 인 이유는, 도둑이 물건을 두고 오거나 물건을 가져오거나 둘 중 하나이기 때문. (물건 하나를 여러 조각으로 나눠서 담을 수 없음)
Fractional Knapsack Problem
조건은 똑같지만, 도둑이 물건의 조각(부분)을 가져갈 수 있음
Fractional Knapsack Problem은 파운드당 값어치를 비교해서 가장 최선의 선택을 하여 Greedy를 적용할 수 있으나, 0-1 Knapsack Problem은 Greedy 적용 불가!
Problem 2: Huffman Codes
데이터 압축 방식으로, Greedy 알고리즘 기반이다.
한줄로 요약하자면, 최적의 prefix code를 위해 Full Binary Tree를 만드는 것으로 정리할 수 있다.
데이터를 encoding/decoding 하는 방법은 아래와 같다.
기본적으로 binary character code(=코드)를 활용하며, 특별한 binary string인 codeword로 디코딩한다.
아래와 같은 두 가지 방식의 코드가 있다.
- Fixed-Length Code
고정 길이 방식의 코드로 인코딩하는 방식으로, 모든 character(문자)들이 동일한 길이의 바이너리 코드로 사용된다.
하지만, 고정 길이 코드는 비효율적인 것이, 불필요하게 많은 메모리를 차지한다. 이유는 가변길이코드 설명에서 이어진다. - Variable-Length Code
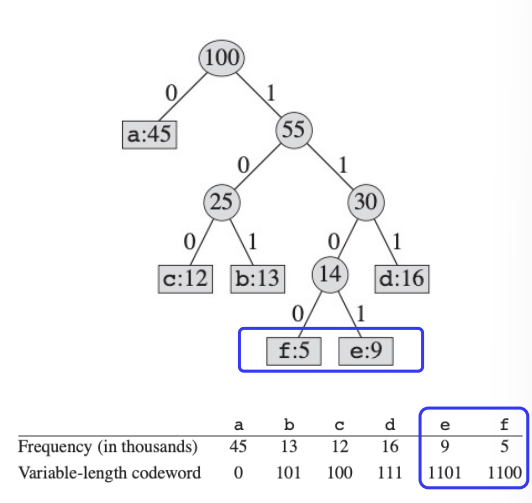
가변 길이 방식의 코드로 인코딩하는 방식으로, 빈도가 가장 높은 문자가 1bit의 codeword를 가지고, 더 빈도가 낮아질수록, 2bit/3bit/… 의 긴 codeword를 가진다.
이를 통해, 인코딩/디코딩에 사용되는 메모리 공간을 줄여, 효율적으로 작동하게 한다.
Prefix Codes
만약, ‘a’가 0이고, ‘b’가 01이고, ‘c’가 1이라고 하면,
001의 디코딩은 0|01 (ab) 인지, 0|0|1 (aac) 인지, 애매모호하고 디코딩되는 상황이 발생한다. 즉, codeword가 ambiguous해질 수 있다.
따라서, prefix code는 어떠한 codeword도 다른 codeword의 prefix가 될 수 없도록 하는 코드이다.
즉, 한 문자의 codeword를 prefix로 가지는 어떠한 codeword도 없다는 것이다.
만약, 최빈 문자인 ‘a’가 0을 codeword로 가진다면, 다른 어떠한 문자도 0으로 시작할 수 없다.
이러한 Prefix Code와 Variable-length Code를 가지는 코드의 codeword를 최적으로 설계하는 방법은 Greedy로 해결하며, Full Binary Tree(모든 node의 child가 2개 or 0개인 트리) 자료구조를 활용한다.
Prefix Codes as a Full Binary Tree
문자에 대해서 binary prefix code는 Binary Tree 상의 root node에서 leaf node까지의 simple path로 해석할 수 있다.
데이터에 대한 최적의 코드는 항상 Full Binary Tree 형태로 나타난다.
왜냐면, 빈번하게 사용되는 문자일수록, root 노드에 더 가까운 leaf 노드로 놓여지기 때문이다. 이렇게 되면, C개의 문자들로 구성된 문자 집합에 대해서 Full Binary Tree가 있다면, C개의 Leaf node와 (C-1)개의 Internal node(당연히 root 포함임)로 구성된다.
Cost of Tree for Codewords
어떤 트리 T를 통해 데이터를 Binary \(B(T) = \sum_{c \in C} c.freq \times d_T(c)\)
$c.freq$는 문자 c의 빈도를 나타내는 값이고,
$d_T(c)$는 c에 대한 codeword의 길이를 나타내는 값, 즉 leaf node의 깊이를 뜻하기도 한다.
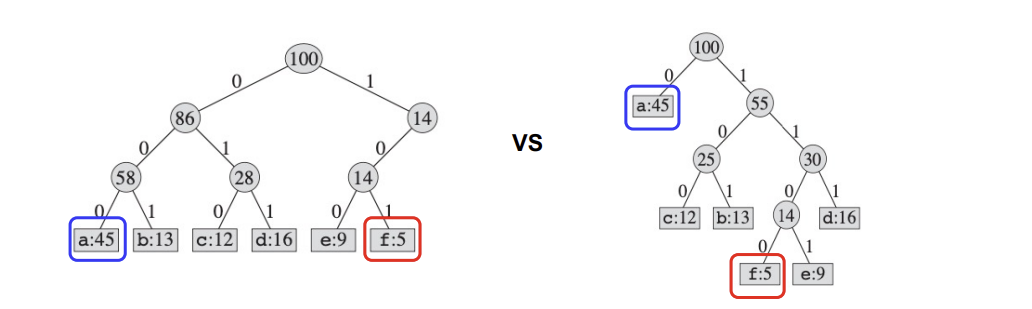
왼쪽 트리는 Fixed-length code(모든 leaf node 까지의 depth가 같다)이고, 오른쪽은 Variable-length code이다.
즉, 우리의 목표는 Full binary tree를 만들어 B(T)를 최소화하는 쪽으로 설계하는 것이다.
Methodology of the Greedy Algorithm
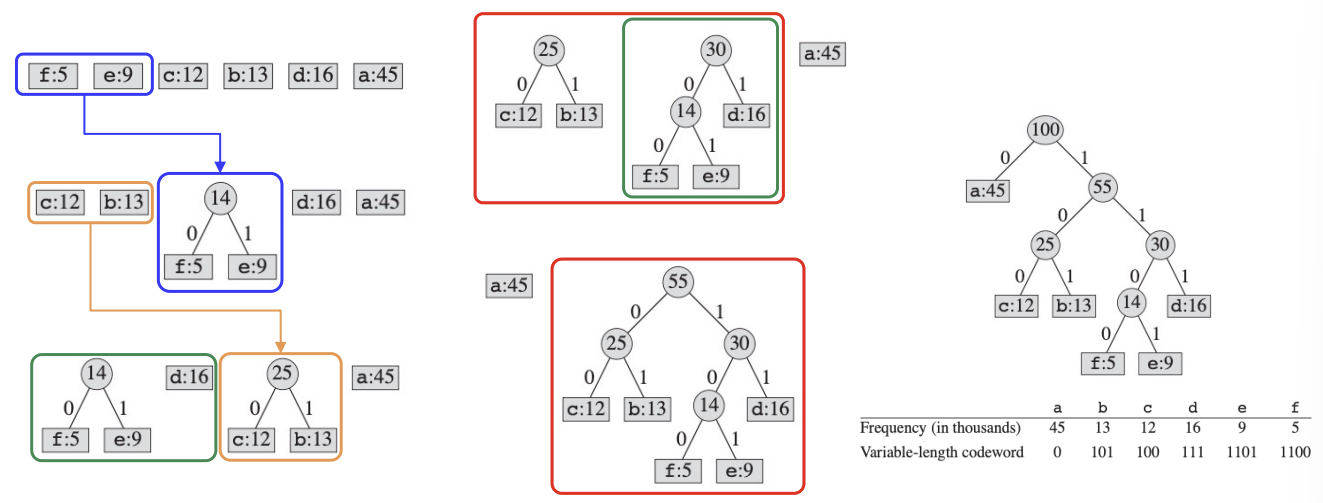
C개의 leaf node로 시작해서, (C-1)개의 합치는 연산을 통해 Full binary tree를 만든다.
여기서 Greedy Choice가 들어가는데, 가장 빈도가 낮은 두 character를 맨 처음 merge 시킨다.(문자(C)들은 min-priority queue인 Q에 저장되고, Q를 통해 최소 빈도 문자 2개를 꺼낸다.)
HUFFMAN(C)
n = |C|
Q = C
for i=1 to n-1
allocate a new node z
z.left = x = EXTRACT-MIN(Q)
z.right = y = EXTRACT-MIN(Q)
z.freq = x.freq + y.freq
INSERT(Q, z)
return EXTRACT-MIN(Q)
총 시간복잡도: $O(n \lg n)$
- min heap 생성: $O(n)$
- Merge & Min-heapify: $O(n \lg n)$
알고리즘은 (n-1)번 merging 연산을 수행하고, 각 merging operation에 대해서 Min-Heapify를 수행한다.
Correctness of the Greedy Algorithm
Greedy의 Correctness를 파악하기 위해,
- Greedy-choice property
- Optimal substructure
두 가지를 만족하는지 파악해야 한다.
Lemma 1) Greedy-Choice Property
C를 문자들 집합이라고 할 때,
x와 y를 가장 적은 빈도로 나타난 두 개의 문자라고 가정하자.
x와 y에 대한 codeword가 동일한 길이를 가지면서 마지막 bit만 다른, C에 대한 prefix code가 존재한다.
이때, 임의의 최적의 prefix code tree T가 있고,
문자 x와 y가 가장 깊은 위치의 형제 leaf 노드로 나타나는 다른 최적의 prefix code tree를 만들도록 수정하는 방식으로 증명한다.
Lemma 2) Optimal Substructure
x와 y가 C에서 가장 적은 빈도를 나타내는 문자라고 했을 때,
$C’ = C - \{x, y\} \cup \{z\}$이며, 이때 z.freq = x.freq + y.freq 이다.
T’을 C’의 최적 prefix code tree라고 했을 때, C에 대한 최적 prefix code tree인 T는 T’으로 부터 도출된다.