[Algorithm] 08. Amortized Analysis(분할 상환 분석)

Introduction to Amortized Analysis

임의의 알고리즘이 어떤 연산은 느리지만, 대부분 빠른 연산을 수행한다면,
일련의 연산들로 구성된 알고리즘의 대표적인 시간을 구하는 것이 힘들다.
점근적 분석을 활용해 worst-case 또는 avg-case를 통해서 대표성을 나타내기 힘들다.
따라서, 상황에 따라 성능이 크게 변동하는 연산 또는 알고리즘의 최악의 경우에도 평균적인 성능을 측정하여 시간 복잡도를 구하는 방법이다.

빠른 연산에 비용이 큰(=느린) 연산의 비용을 흩뿌리는(나눠주는) 아이디어를 통해 분석을 수행하며, 일련의 연산을 수행하는데 필요한 비용을 평균을 내는 개념으로 이해하면 쉽다.
즉, worst case 에서도 각 연산의 평균적인 성능을 보장한다.

실제 Build-Max-Heap을 살펴보았을 때,
worst-case 시간 복잡도는 매우 비관적인(Pessimistic) 분석을 내놓는다.

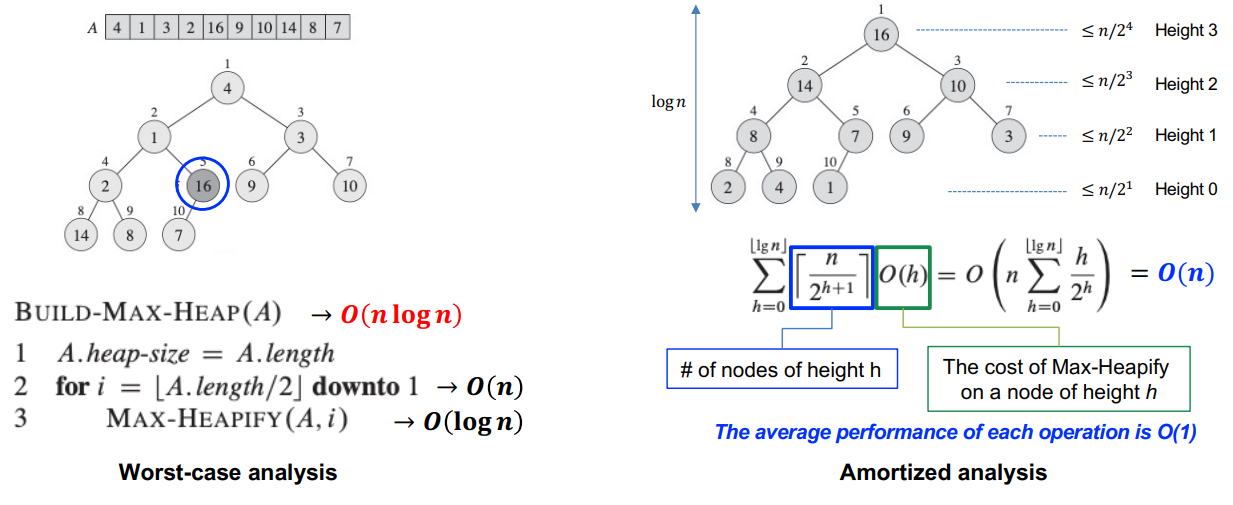
그렇다면, Avg-case Analysis(평균 성능 분석)와 무엇이 다른가?

1. Avg-case Analysis는 입력 데이터의 확률 분포 개념을 필요로 한다.
2. Worst-case Analysis나 Amortized Analysis에 비해서 분석하는 방식이 매우 복잡하다.

Amortized Analysis는 확률 분포 개념을 미포함하며, worst-case에서도 각 연산의 평균적인 성능을 제공하기 때문에 더욱 정확하고, 효율적인 알고리즘을 설계하는데 유용하다는 이점이 있다.

Amortized Analysis의 방식에는 세 가지가 있다.

1. Aggregate Analysis
2. Accounting Method
3. Potential Method

이 세 가지 방식을 각각 두 가지 예제에 적용시켜 볼 것이다.

1. MULTIPOP이 추가된 스택 설계
2. INCREMENT라는 비트 단위 연산을 0부터 카운트 업하는 Binary Counter 설계

Aggregate Analysis

1. T(n): 최악의 경우에 n개의 일련의 연산을 수행하는데 드는 총 비용을 계산한다.
2. T(n)의 평균을 냄으로써, 각 연산에 대한 amortized cost를 결정한다.
   각 연산 당, amortized cost는 T(n)/n으로 계산한다.
   연산의 종류가 여러 가지 있을 때도, 모든 연산에 amortized cost를 적용시킨다.

즉, worst-case analysis보다 total cost에 대한 더 나은 uppder bound를 얻을 수 있다.

Ex 1) Stack with Multipop

일반적인 Push(S, x)과 Pop(S)의 경우 $O(1)$의 시간 복잡도를 가지는 것은 자명하고,
Multipop(S, k)는 스택 S에서 top-k elements를 pop 하는 연산인데,
이에 대한 비용은 꺼내려는 k개의 원소 개수에 따라서 결정된다. $O(k)$

<Push, Push, Pop, Push, Multipop(2), …, Multipop(3), Pop>
이러한 n개의 연산이 있다고 가정하면, total cost가 얼마일까?

우선, Worst-Case Analysis를 수행해보자.
Multipop 연산은 input 크기가 n이 최대이므로(스택이 가득 찬 경우를 말한다), $O(n)$의 시간복잡도를 가지며, 이러한 Multipop 연산 n개가 있을 수 있으므로, 총 $O(n^2)$의 시간복잡도를 가진다고 계산한다.
근데, 과연 정확한 값일까? 절대 아니다.
Multipop은 우선, n번 수행할 수 없다. Multipop(n)을 한번 수행하면, n개의 element가 있던 스택은 empty 상태가 되어, Multipop(n)을 절대 수행할 수 없다.

따라서, Amortized Analysis를 수행해야 한다.
Aggregate Analysis로 계산해보자.
원소는 스택이 비어있지 않을 때만 스택에서 pop이 가능하다는 사실을 바탕으로, 아래와 같은 사실을 알 수 있다.
Pop 연산의 횟수는 최대 Push 연산의 수까지 가질 수 있다.
$Pop\,횟수 \leq Push\,횟수 \leq n$ 이므로, $Pop\,횟수 + Push\,횟수 \leq 2n$으로 나타낼 수 있다.
따라서, 아무리 해도 n개의 Operation에 대한 시간 복잡도는 $O(n)$을 넘길 수 없다.
즉, 총 비용은 $O(n)$이고, amortized cost는 $O(n)/n=O(1)$이다.

MULTIPOP(S, k)  
  while not STACK-EMPTY(S) and k > 0
    POP(S)
    k = k-1

Ex 2) Binary Counter

Incrementing Binary Counter 문제이고, k-bit의 Binary counter를 구현한다고 가정해보자.
우측 맨 끝을 0부터 시작해서, A[0, 1, …, k-1]의 배열이 counter로서 역할을 한다.
e.g. INCREMENT(좌측이 Highest-order bit, 우측이 Lowest-order bit)

Counter Value	A[k-1]	…	A[2]	A[1]	A[0]
0	0	…	0	0	0
1	0	…	0	0	1
2	0	…	0	1	0
3	0	…	0	1	1
4	0	…	1	0	0
5	0	…	1	0	1
6	0	…	1	1	0

INCREMENT(A)
  i = 0
  while i < A.length and A[i] == 1
    A[i] = 0  //O(1)
    i = i + 1
  if i < A.length  
    A[i] = 1  //O(1)

INCREMENT 연산의 비용은 bit flip 횟수에 비례한다.
그리고 bit flip 횟수는 counter value에 의존하는 값이다.

그렇다면, n번의 INCREMENT 연산의 upper bound는 어떻게 구할까?
우선, Worst-case Analysis에서는 $O(nk)$의 시간복잡도를 따른다.
하지만, 이는 tight upper bound가 아님.

Counter Value	A[3]	A[2]	A[1]	A[0]	Cost	Total Cost
0	0	0	0	0	0	0
1	0	0	0	1	1	1
2	0	0	1	0	2	3
3	0	0	1	1	1	4
4	0	1	0	0	3	7
5	0	1	0	1	1	8
6	0	1	1	0	2	10
7	0	1	1	1	1	11
8	1	0	0	0	4	15

A[0]에서는 n번의 bit flip이 일어나고,
A[1]에서는 n/2번의 bit flip이 일어나며,
A[2]에서는 n/4번의 bit flip이 일어나므로,
이를 합하면 다음과 같은 수식을 얻을 수 있다.

\[\sum_{i=0}^{k-1} \lfloor \frac{n}{2^i} \rfloor < n \sum_{i=0}^{\infty}\frac{1}{2^i} = 2n\]

따라서, total cost는 $O(n)$이고, Amortized cost per operation 은 $O(n)/n = O(1)$

Accounting Method

aggregate analysis와는 다르게, 다른 종류의 연산에 다른 amortized costs를 할당한다.
Aggregate Analysis: Amortized costs가 연산 종류가 달라도 모두 동일
Accounting Method: Amortized costs가 연산 종류에 따라 달라짐

Credit 개념을 도입해서, 일종의 prepaid cost를 계산함.
amortized cost ($\hat c$)와 actual cost $c$의

Ex 1) Stack with Multipop

Ex 2) Binary Counter

Potential Method

Ex 1) Stack with Multipop

Ex 2) Binary Counter

Dynamic Tables