[Algorithm] 09. Graph Algorithms(DFS, BFS)

그래프와 그래프 탐색 알고리즘인, DFS와 BFS 알고리즘에 대해 다룹니다.

Posted Jun 5, 2025 Updated Jun 10, 2025

graph_intro

By Youngbeom Cho

views 16 min read

Introduction to Graphs

Definition & Applications

그래프란 entity와 그 entity 간의 relation를 표현하는 일반적인 언어이다.

적용 예시: Social Network Analysis, Digital Healthcare, RecSys, Social Welfare, RAG 등

Terminologies

G(V, E)로 정의하며, V는 Vertex (정점, 노드)이고, E는 Edge (간선)이다.
즉, V는 Entity 집합, E는 Relation의 집합을 의미한다.

Directed Graph vs. Undirected Graph

Directed Graph: Edge에 방향성이 존재한다. 만약, 어떤 edge를 (u, v)로 나타내면, u는 v에 adjacent하다고 표현할 수 있다. (단, v가 u에 adjacent하다고 표현하진 못한다. 이는 Asymmetric한 특징을 나타낸다.)
Undirected Graph: Edge에 방향성이 없다. 만약, 어떤 edge를 (u, v)로 나타내면, u는 v에 adjacent하다고 표현할 수 있다. 반대로 v도 u에 adjacent하다고 표현할 수 있다. (Symmetric한 특징이 드러난다.)

Degree of a Node(노드 또는 정점의 차수)
쉽게 설명하면, 꼭지점(정점, 노드)에 입사하는 모서리(간선)의 개수이다.
이는 Directed인지, Undirected 인지에 따라 다르게 계산될 수 있다.

Directed Graph
- In-degree of a node: 해당 노드에서 incoming edges의 개수이다.
- Out-degree of a node: 해당 노드에서 outcoming edges의 개수이다.(바깥 방향을 향하는 간선의 개수)
Undirected Graph
해당 노드(정점)에 연결된 간선의 개수이다.

Path(경로)
vertex u에서 vertex v로 가는 path(경로)는 $<v_0, v_1, \dots, v_k>$로 나타낸다. 이때, $v_0$는 u, $v_k$는 v로 볼 수 있다.
vertices에 대한 sequence의 길이(length)는 path(경로)에서 지나가는 edge의 개수로 나타낸다.
만약 vertex u에서 v까지 path가 있다면, reachable하다고 표현한다.
simple path란, path상의 모든 정점이 distinct한 path로, cycle 없이(=중복되는 vertex)없이 path가 만들어진 경우를 말한다.
해당 그래프를 통해 생성되는 모든 path가 simple한 경우, 즉 cycle이 존재하지 않는 graph를 Acyclic Graph라고 표현한다.

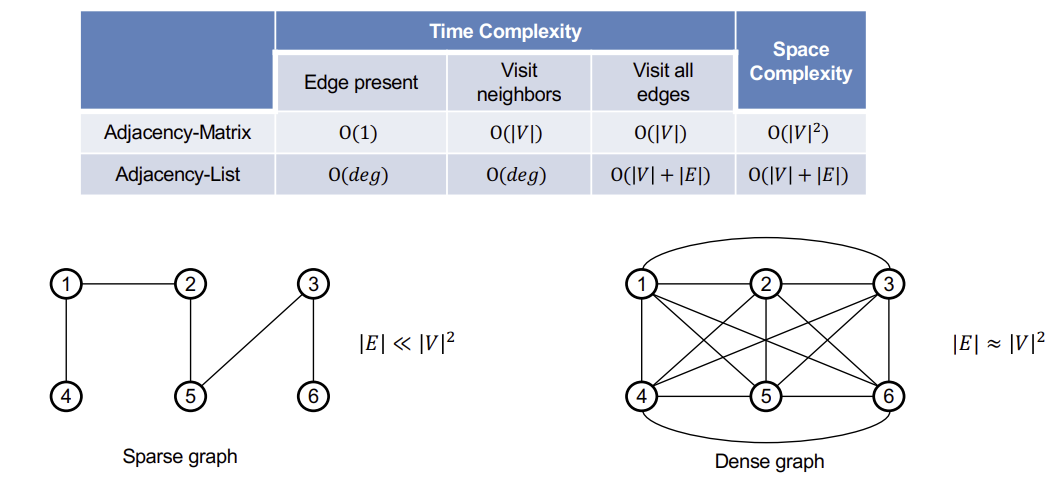
Representation

Graph를 표현하는 방법엔 두 가지가 있다.

Matrix
List

딱 봐도, 뭐가 더 효율적일지 보인다.
결국 List를 활용해서 DFS나 BFS를 설명하겠지만, Matrix로 표현하는 방법도 있다는 것을 알아두고, 왜 Matrix가 더 비효율적인지 살펴볼 필요도 있다.

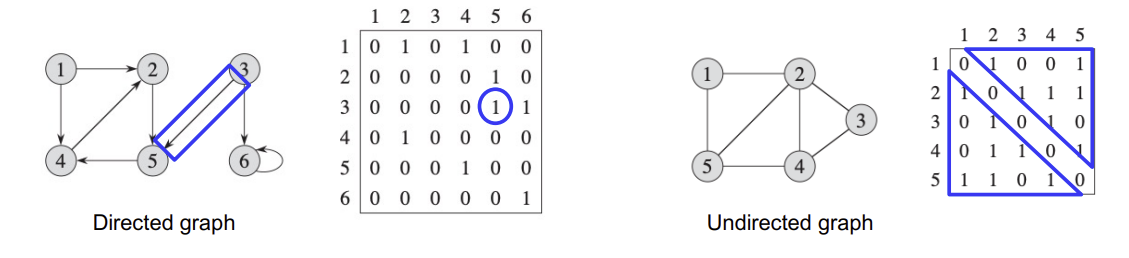
Adjacency-Matrix Representation
$|V| \times |V|$인 matrix A가 있을 때,
vertex i에서 vertex j로 연결된 edge가 존재하면 A[i][j]의 값은 1로 표시하는 방법이다.
특이한 점은, Undirected Graph의 경우 A의 대각선(diagonal)에 대하여 symmetric하다.

공간복잡도
$O(|V|^2)$
Vertex 개수의 제곱만큼의 공간을 가진다.
Matrix이고 존재하지 않는 edge에는 0으로 채우기 때문이다.

시간복잡도
기본적으로 $O(|V|^2)$를 가진다.
연산 종류에 따라 다르지만, Edge가 존재하는지를 따지려면, $O(1)$이 필요.
해당 Vertex의 Neighbor edge 판단하려면, $O(V)$이 필요.
모든 edge를 탐색하려면, $O(|V|^2)$가 필요하다.

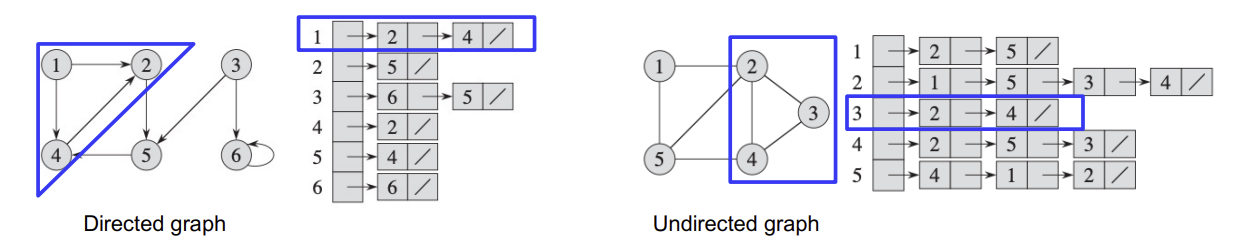
Adjacency-List Representation

$|V|$개의 List를 가지고, 각각의 리스트는 하나의 vertex에 대응한다.
vertex u에 대해서, u의 adjacency list에는 adjacent vertices를 포함한다.

공간복잡도
$O(|V|+|E|)$
존재하는 edge만 보관함

시간복잡도
$O(|E|)$
Edge가 존재하는지 A[i][j]를 확인, O(vertex i의 차수)
이웃 리스트 -> O(vertex의 차수)
모든 엣지를 탐색 $O(|E|)$

모든 트리는 그래프지만, 모든 그래프는 트리는 아니다.
그래프는 만약 cycle 없고, 모든 vertice가 연결되어있다면 트리가 될 수 있다.

Searching on Graphs

왜 우리는 Graph Searching 알고리즘이 필요할까?
그래프에서 특정 vertex를 찾고, 특정 vertex까지 reachable 한지를 파악하고, shortest path를 찾는 다양한 문제를 풀기 위함이다.

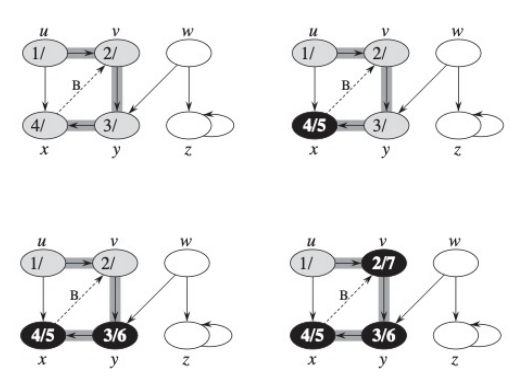
BFS(Breath-First Search)

$G=(V, E)$를 가지는 그래프와 source vertex(시작 정점) s가 주어지면,
s로부터 모든 reachable(도달가능)한 vertex를 discover한다.

Discover의 의미는 source vertex에서 distance(거리)를 점점 증가시키면서 탐색하는 것을 의미한다. Breath-First라는 이름에서 알 수 있듯이 가까운 vertex 먼저 탐색하는 알고리즘이다.
(cf. 이때, distance의 의미는 임의의 정점 u에서 v까지의 최단 경로를 말한다.)

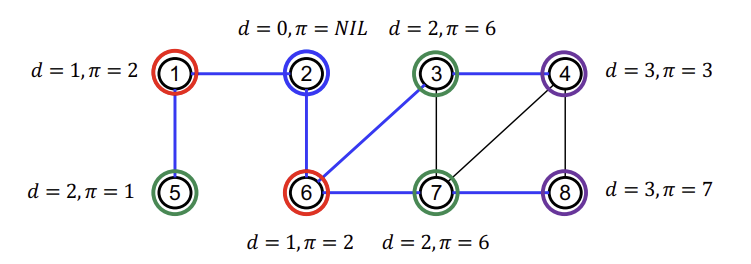
BFS의 특징은 항상 해당 vertex에서 시작 정점으로부터의 거리 $d$와 해당 vertex가 이전에 지나온 vertex (즉, predecessor)인 $\pi$를 항상 연산해야 한다.

BFS(G, s)
  // source vertex를 제외한 vertex에 초기화
  for each vertex u ∈ G.V-{s}
    u.color = WHITE
    u.d = ∞
    u.π = NIL
  // WHITE는 아직 discover하지 않은 것 (= enqueue 대상)
  // GRAY는 Discover했지만, 끝나지 않은 것 (= 아직 Q에 있는 상태)
  // BLACK은 완전히 Finished된 것 (= dequeue 된 것)
  s.color = GRAY
  s.d = 0
  s.π = NIL
  Q = ∅   //Queue 자료구조 활용
  ENQUEUE(Q, s)
  while Q != ∅              //Explorer a Graph
    u = DEQUEUE(Q)
    for each v ∈ G.Adj[u]   //Adj linked-list 참고. u에 대해서!
      if v.color == WHITE
        v.color = GRAY
        v.d = u.d + 1
        v.π = u
        ENQUEUE(Q, v)
    u.color = BLACK

BFS의 시간복잡도
Initialization: $O(|V|)$
Exploring a graph: $O(|V| + |E|)$
모든 vertex는 최대 1번 enqueue됨
모든 Adjacency list는 최대 1번 scan됨

BFS Tree

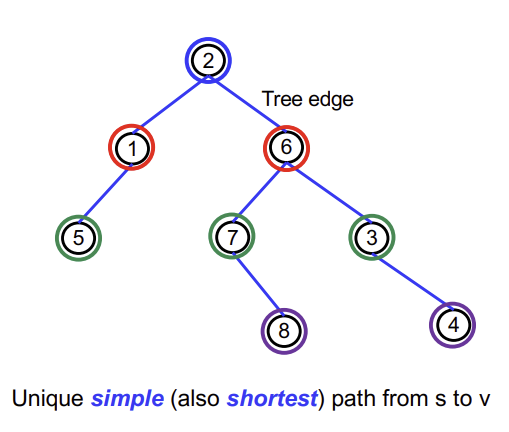
G에 대한 Predecessor Subgraph인 $G_{\pi} = (V_{\pi}, E_{\pi})$
$V_{\pi} = {v \in V: v.\pi \neq NIL} \cup \{s\}$
$E_{\pi} = {(v.\pi, v): v \in V_{\pi} = \{s\}}$

위 그림 및 집합으로 정의될 수 있다.
또한, tree의 Edge 개수인 $|E_{\pi}|$는 $|V_{\pi} - 1|$인 특징을 보인다. (당연히 트리니까..)

만약, Adajacency list가 아닌 Matrix 방식으로 표현한다면,
시간복잡도는 Initialization에서 $O(|V|^2)$로 바뀌고,
Exploring a graph에서 $O(|V|+|V|^2)$로 바뀐다.
필요없는 0까지 martix에서 scanning 해야 하는 시간낭비가 일어난다.
특히, 수도코드 상에서 for each v in G.Adj[u]부분이

for v = 1 to |G.V|       // 모든 정점 v에 대해
  if G[u][v] == 1        // u와 v가 연결되어 있으면 (간선이 존재하면)

위처럼 바뀐다.

DFS

$G=(V, E)$를 가지는 그래프가 주어지면,
언제든 가능한만큼 그래프에서 deeper하게 탐색하는 알고리즘이다.

deeper의 의미에서 알 수 있듯이, 정점을 하나 선택해 가능한 가장 깊은 정점까지 탐색한 후 인접한 정점으로 이동해 다시 깊게 탐색하는 알고리즘으로, BFS보다 조금 생소하고 어렵게 느껴지는 알고리즘이다.

각 vertex는 다음 두 개의 timestamps를 가진다.
v.d: discovery time
v.f: finish time

DFS 메인 함수

DFS(G)
  // 모든 vertex 초기화
  for each vertex u ∈ G.V
    u.color = WHITE
    u.π = NIL
  time = 0
  // 모든 vertex (WHITE인) 대상으로 DFS-VISIT 수행
  for each vertex u ∈ G.V
    if u.color == WHITE
      DFS-VISIT(G, u)

DFS 탐색 함수 - DFS-VISIT

DFS-VISIT(G, u)
  // Discovered  
  time = time + 1
  u.d = time
  u.color = GRAY
  // 재귀적으로 deeper한 이웃 정점을 방문
  for each v ∈ G.Adj[u]
    if v.color == WHITE
      v.π = u
      DFS-VISIT(G, v)
  // 재귀 호출 전부 완료되면 하나씩 Finish time 정의
  u.color = BLACK
  time = time + 1
  u.f = time

DFS의 시간복잡도
Initialization: $\Theta(|V|)$
Exploring a graph: $\Theta(|V|+|E|)$
Aggregate Analysis에 의해서 $O(|V|*|E|)$가 아님을 알 수 있음.

DFS의 특징

Depth-First Forest
predecessor의 subgraph는 여러 개의 Tree들로 구성된 forest를 만든다.
Descendant
v가 u의 descendant인 것은 v가 u가 GREY인 시간 동안 discover 됨을 의미한다.
Parenthesis Structure
어떠한 DFS에서도, 모든 두 개의 vertex에 대해서, 아래 세 가지 조건 중 하나는 성립한다.
1) 임의의 두 vertex u, v에 대해서 [u.d, u.f]와 [v.d, v.f]의 시간 간격이 완전히 분리된 구간에 있으면, depth-first forest에서 서로 다른 트리에 속해 있음을 의미한다. (u, v가 둘 중 어느 것도 다른 것의 descendant가 될 수 없음)
2) [u.d, u.f]에서의 시간 간격이 [v.d, v.f]의 시간 간격 안에 포함된다면, u는 v의 descendant이다.
3) [v.d, v.f]에서의 시간 간격이 [u.d, u.f]의 시간 간격 안에 포함된다면, v는 u의 descendant이다.

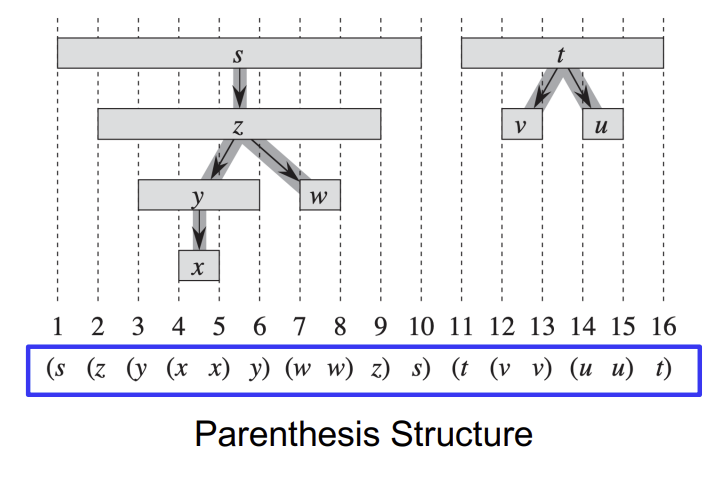
Edge의 분류

Tree Edge depth-first forest에 속하는 edge
즉, DFS 수행 중에 실제로 방문을 유도한 edge
새 정점을 발견할 때 사용된 edge
Back Edge Nontree edge이면서, 한 정점에서 자신의 ancestor로 가는 edge
Back Edge가 있으면, Cycle이 존재한다.
Forward Edge Nontree edge이면서, 한 정점에서 이미 방문한 descendant로 가는 edge
쉽게 말해, 조상에서 자손으로 다이렉트로 가는 edge이다.
Cross Edge 서로 조상-자손 관계가 없는 정점 사이를 잇는 간선

일반적으로 분류는 WHITE, GRAY, BLACK의 색깔로 그냥 tree edge인지, back edge인지, forward/cross edge인지 나누는 방식으로 진행된다.
예를 들어, Black이 된 vertex에서 조상 vertex(GRAY vertex)로 가는 edge가 있다면 Back Edge로 판단한다.
혹은 조상 vertex(GRAY vertex)에서 이미 Black처리된 자손 vertex로 가는 edge는 forward edge로 판단한다.

Applications

Connected components

undirected graph에서 connected component는 노드 집합에서 모든 노드 쌍 간에 path가 만들어지는 가장 큰 노드 집합을 말한다.
예를 들면, 어떤 노드는 다른 노드들에 reachable한 상황을 말한다.
이러한 Connected component를 식별하는 방법은 DFS를 돌리는 것이다.
DFS를 돌리면 depth-first forest가 만들어지고, 그래프 G가 connected component를 가진 많은 트리로 구성되었음을 확인할 수 있기 때문이다.

DFS와 DFS-VISIT 소스코드에서
cc 속성과 k를 변수로 추가하여, 동일한 connected component에 있는지, 총 몇 개의 vertex들이 연결되었는지 파악한다.

Topological sort

DAG(Directed Acyclic Graph)가 주어지면, 그래프 내의 모든 vertex에 대해서 linear ordering을 생성한다.
이때, 그래프 G가 edge(u, v)를 가진다면, u는 v가 ordering 되기 전에 나타나야 한다.

DAG는 이벤트 간의 선후관계나 의존성을 파악하는 application들에 주로 이용된다.

Topological Sort의 필요조건
만약 cycle이 있다면, linear ordering이 불가능하다.
그러면 Acyclic 증명해야 하고, 이는 DFS를 이용해 Back Edge 있으면 Acyclic 아님 (=cycle 있음)을 증명하자.

Topological Sort 문제 해결 방법

0 in-degree를 가지는 것을 left에서부터 배치한다.
그래프 G에 대해서 DFS를 돌리고, finishing time의 오름차순으로 오른쪽에서부터 채운다.

Computer Science, Algorithm

This post is licensed under CC BY 4.0 by the author.