[Algorithm] 11. Shortest Path (1): Dijkstra's Algorithm
다익스트라 알고리즘에 대해 다룹니다.
Shortest Path
Problem Definition
directed graph G=(V, E)와 가중치 함수 w: $E \to \mathbb{R}$에 매핑된 실수값의 가중치를 가지는 edge(간선)이 주어지면,
Weight of path(경로에 대한 가중치)는 경로 p가 $p=<v_0, v_1, …, v_k>$를 만족할 때,
위와 같이 계산된다.
즉, 지나갔던 edge의 weight를 싸그리 더해주면 된다.
shortest-path weight(최단 경로의 가중치)는 u에서 v까지의 경로라고 할 때, 다음과 같이 구한다.
\[\delta(u, v) = \left\{\begin{array}{ll} min\{w(p): u \overset{p}{\rightsquigarrow} v \} \quad \text{if there is a path from u to v} \\ \infty \quad \text{otherwise.} \end{array}\right.\]따라서, shortest path(u에서 v까지)는 아래와 같은 수식을 만족함으로써 정의된다.
\[w(p) = \delta(u, v)\]위에서 정의했던 path에 대한 가중치 합과 shortest-path weight가 같은 값을 가지면 된다.
shortest path는 반드시 unique할 필요가 없다.
즉, 최단 경로는 유일하지 않으며, 여러 경로가 동일한 shortest path를 가질 수 있다.
Shortest Path: Variants(최단 경로 문제의 다양한 유형)
- SSSP(Single-Source Shortest-Paths)
주어진 하나의 source vertex(시작 정점) s에서 모든 다른 정점(v)까지 최단 경로를 찾는 문제
해결 알고리즘) 다익스트라 알고리즘, 벨만-포드 알고리즘 - Single-Destination Shortest-Paths
모든 정점 v에서 특정 destination vertex(도착 정점)까지의 최단 경로를 찾는 문제 그래프의 방향성이 없다면 SSSP 문제로 변형하여 푼다! - Single-Pair Shortest-Path
정해진 두 정점(u와 v)사이의 단일 최단 경로를 찾는 문제, 그냥 쉽게 쉽게 u->v만 구하면 됨. - All-pair Shortest-Paths
모든 정점 쌍 (u, v)에 대해 모든 최단 경로를 찾는 문제
해결 알고리즘) Floyd-Warshall, 여러 번 다익스트라 적용
Shortest Path: Condition(최단 경로 문제의 조건)
Shortest Path를 풀 때, 중요한 점은 Cycle의 유무나 Edge의 weight가 음수인 경우일 것이다.
나중에 음의 간선의 존재 여부 등으로 다익스트라이냐 벨만포드냐로 나누긴 하겠지만,
Shortest Path라는 큰 그림에서 보자면,
Negative-weight cycle(음의 사이클)을 절대 허용하지 않는다.
일반적으로는 음의 간선이 존재하도 되며, cycle이 존재해도 된다.
하지만, 해당 사이클로 얻어지는 가중치 합이 음수가 되는 음의 사이클이 존재한다면 이는 허용하지 않는다. 결국, 해당 사이클을 계속 돌아 가중치 음의 무한대로 가버려 최단 경로를 구할 수 없게 된다.
Optimal Substructure
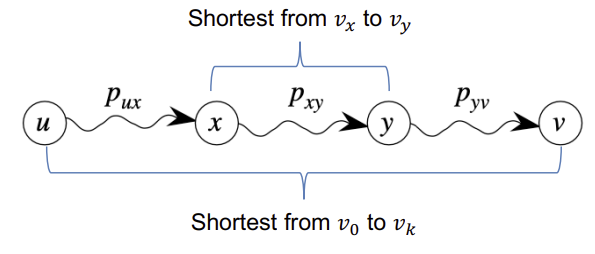
Lemma 1: Subpaths of shortest paths are shortest paths
최단 경로의 subpath(하위 경로)도 최단 경로이다.
Pf.
path p가 최단경로이고, $u \overset{p_{ux}}{\rightarrow} x \overset{p_{xy}}{\rightarrow} y \overset{p_{yv}}{\rightarrow} $로 둘 때,
$w(p) = w(p_{ux}) + w(p_{xy}) + w(p_{yv})$라고 할 수 있는데,
만약, $p’{xy}$가 $w(p’{xy}) < w(p_{xy})$와 같이 더 가중치가 작은 path가 중간에 들어가서 더 짧은 전체 경로를 만든다면, p는 최단 경로가 아니게 되므로, 초기 가정을 부정하는 모순점이 발생.
Output
- shortest-path weights(최단 경로의 가중치)
- vertices on shortest paths(최단 경로가 지난 정점들)
따라서, 각 정점(vertex)는 v.d와 v.π를 속성으로 가진다.
v.d: 최단 경로 추정값으로, 최단경로를 구하는 동안 $v.d \geq \delta(s, v)$를 만족한다.
v.π: s부터의 최단 경로 상에서 predecessor(전임 정점)
두 가지 값을 표시한다.
Process & Properties
일반적인 SSSP 알고리즘의 과정은 다음 두 가지 단계를 거쳐 진행된다.
- Initialization: INIT-SINGLE-SOURCE 함수로 알고리즘이 시작됨
각 정점(vertex)에서의 shortest-path estimate 값을 초기화하고, predecessor도 초기화한다.1 2 3 4 5
INIT-SINGLE-SOURCE for each v ∈ G.V v.d = ∞ v.π = NIL s.d = 0
- Relaxation: edge(간선)을
Relaxing함으로써 각 vertex(정점)에 대한 shortest-path estimate인v.d를 반복적으로 업데이트한다.1 2 3 4
RELAX(u, v, w) if v.d > u.d + w(u, v) v.d = u.d + w(u, v) v.π = u
즉, 정리하면, edge(u, v)를 지나는 더 짧은 경로가 있다면, shortest-path estimate와 predecessor를 업데이트한다. 이것을 Relaxing한다고 표현한다.
최단 경로 문제는 다음과 같은 특성을 지닌다.
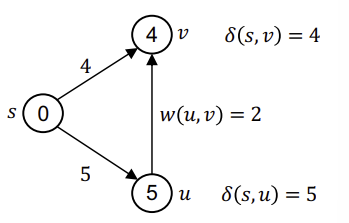
- Triangle Inequality
어떠한 edge(u, v)에 대해서, $\delta(s, v) \geq \delta(s, u) + w(u, v)$를 만족한다.
- Upper-Bound Property
모든 $v.d \leq \delta(s, v)$ 이와 같은 식을 항상 만족하며, 한번 $v.d = \delta(s,v)$ 가 되었다면, 절대 바뀌지 않는다. - Path Relaxation Property
path p가 $v_0$부터 $v_k$까지의 최단경로라고 가정한다면, $(v_0, v_1)$, $(v_1, v_2)$, …, $(v_{k-1}, v_k)$ 순서로 p에 대한 edge를 relaxing해준다. 그러면, $v_k.d = \delta(s, v)$ s처럼, $v_k$에서의 shortest-path estimate 값은 s에서 v까지의 최단 경로의 가중치가 된다.
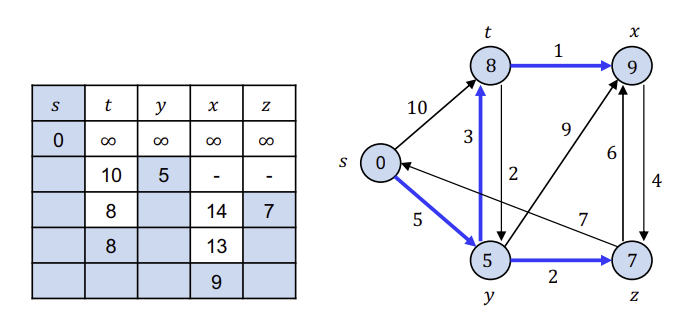
Dijkstra’s Algorithm
source vertex에서 가장 가까운 vertex를 선택해 Greedy Approach를 진행한다.
다익스트라 알고리즘은 모든 간선 가중치가 non-negative한 상황에서만 사용 가능하다.
1
2
3
4
5
6
7
8
9
DIJKSTRA(G, w, s)
INIT-SINGLE-SOURCE(G, s)
S = ∅
Q = G.V // Priority Queue에 정점을 집어넣는다. 당연히 시작 정점 기준 오름차순으로 정렬.(Min-Binary-Heap 씀)
while Q ≠ ∅
u = EXTRACT-MIN(Q)
S = S ∪ {u}
for each vertex v ∈ G.Adj[u]
RELAX(u, v, w)
Time Complexity of Dijkstra
Priority Queue가 구현된 방식에 따라 시간복잡도가 좌우된다.
물론 Array 기반으로 구현되었으면, $O(V^2)$을 가지는데, 이렇게 구현할 필요는 없고, 일반적인 Binary heap 기반 구현을 하면 아래와 같은 시간복잡도를 가진다.
\(O(V \lg V + E \lg V)\)
Extract-Min(Q): $O(\lg V)$
Decrease-Key(Q, v): $O(\lg V)$
Building the min-heap: $O(V)$