[Artificial Intelligence] 02. Search (2): informed search

앞서 살펴봤던 UCS를 informed search에 맞게 알고리즘을 수정해보고, graph search에 대해 알아보자.

1. Informed Search: Heuristics

Heuristic(휴리스틱), $h(x)$: 하나의 상태가 goal(목표)에 얼마나 가까운지를 추정(estimate)하는 함수
특정 탐색 문제를 위해 설계되는 함수이고, manhattan distance, euclidean distance 등이 그 예이다.
다양한 문제에 맞게 휴리스틱 함수를 설계하는 것이 중요하다.

2. Greedy Search

Strategy that select a node with least heuristic value
가장 작은 휴리스틱 값을 가지는 노드를 항상 선택하여 탐색하는 알고리즘이다.
즉, frontier에서 goal state와 가장 가깝다고 생각되는 노드를 선택하여 빠르게 탐색하려는 알고리즘이다.
하지만, 대부분 최적의 결과를 가져다 주지 않고, 최악의 경우 badly-guided DFS처럼 행동한다.
즉, Optimality X, Completeness X

3. A* Search

UCS의 안정성과 Greedy의 효율성을 결합한 알고리즘
$g(n)$: UCS를 통한 축적된 비용. 즉, 과거 비용(backward cost)를 나타냄
$h(n)$: Greedy를 통한 휴리스틱 값이자 goal proximity(목표화 현재 상태의 거리). 즉, 미래 추정 비용(forward cost)를 나타냄
A* search는 위 두 값의 합을 통해 최적의 경로를 탐색한다.
\(f(n) = g(n) + h(n)\): A* 탐색은 두 값의 합이 작은 노드들을 선택하여 탐색하는 것이다.

A* search의 종료

단순히 목표 노드(G)를 프론티어(priority queue)에 enqeue(추가)했을 때 멈추면 안 되고, 목표 노드를 dequeue(꺼낼) 때만 종료해야 함

A* search의 Optimality

항상 optimal하지는 않다.

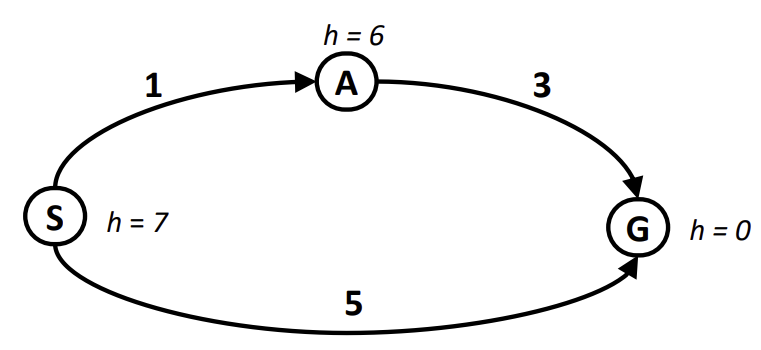
위 예시를 살펴보자.
실제 A* 알고리즘을 돌린다고 가정해보자.
S에서 A와 G로 search tree가 형성될 거고, frontier(priority queue)에는 A와 G가 각각 담길 것이다.
이때, A에서의 f값은 7이고, G에서의 f값은 5이다.
그러면, 우선순위 큐의 규칙에 따라 G가 dequeue되며 A* search는 terminate된다.
즉, optimal한 결과를 도출하지는 않는다.
이유는 휴리스틱 함수의 inadmissible 때문이다.
inadmissible(허용 가능하지 않다는 것)은 실제 비용을 과대평가한다는 것이다.
위 예시를 통해 살펴보면, 실제 A부터 G까지의 비용은 3임에도 휴리스틱은 6이라고 pessimistic하게 평가하고 있다.
따라서, 휴리스틱 함수 설계는 optimistic하게 이뤄져야 하며, 이는 실제 비용보다 더 적게 추정해야 한다는 것을 의미한다.

Admissible Heuristics

1. Inadmissible(=pessimistic) Heuristics
   휴리스틱 함수가 좋은 plan을 frontier에 가둠으로써 optimality를 보장하지 못하는 문제가 발생한다. 앞서 살펴본 예시를 통해 쉽게 확인할 수 있다.
2. Admissible(=optimistic) Heuristics
   따라서, 휴리스틱 함수는 admissible하게 설계하여, 실제 비용을 절대 초과하지 않게 해야 한다.(bad plan의 속도를 늦추는, 우선순위를 밀리게 해야 함)

Admissible(=optimistic) heuristic 함수 h는 아래 조건을 만족해야 한다.(모든 노드 n에 대해서, h*가 n으로부터 가장 가까은 goal state에 대한 실제 비용에 대한 함수라고 가정)
\(0 \geq h(n) \geq h*(n)\)

따라서, admissibility가 휴리스틱 함수에 보장되면, 그 함수를 사용한 A* tree는 항상 최적 해를 찾는다.

만약, 휴리스틱 함수가 constant여도 admissible heuristic이고, 이때의 A* search는 optimal한 결과를 도출함

A* tree search에 대한 optimality에 대한 증명은 생략

정리하자면, UCS와 A의 차이점은 아래 그림과 같다.

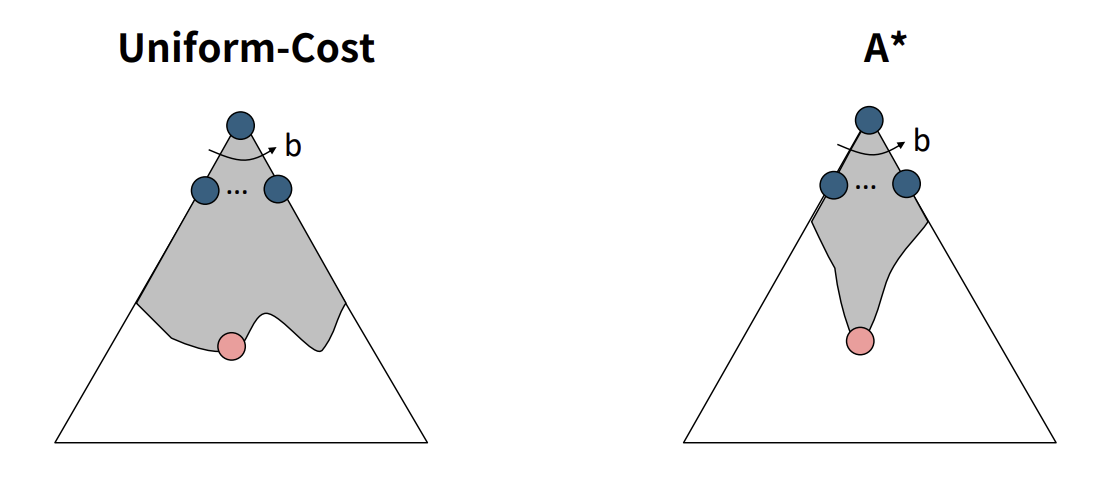
UCS는 모든 방향에 대해서 동등하게 확장한다면, A search는 “heuristic 함수에 기반하여” 주로 goal을 향해 확장하지만, optimality를 보장하기 위해 “실제 비용(greedy)”을 통해 위험을 분산하며 탐색한다.

4. Heuristics Design

휴리스틱 함수의 설계는 admissible한 휴리스틱을 만족해야 한다.
즉, 휴리스틱 함수는 실제 값보다 작거나 같은 값(lower bound)를 만족해야 한다.
따라서, 좋은 휴리스틱 함수를 만들기 위해선, relaxed problem에 대한 해를 찾는 것이라고 설명하는데, 몇 가지 제약 조건을 제거하여 더 단순하게 만든 문제에 대한 해를 구해 휴리스틱 함수로 설정하는 것을 의미한다.
예를 들어, 팩맨 게임에서 ‘벽을 따라 이동해야 한다’는 조건을 제거하거나, 실제 도로에서의 탐색 문제에서 ‘직선으로 날아갈 수 있다’라고 조건을 완화하는 상황이 있을 수 있다.

정리하자면, A* search에서는 휴리스틱 함수를 설계할 때 trade-off가 존재한다.(estimation의 quality와 node 당 work(탐색) 개수)
즉, 얼마나 정확한지와 얼마나 많은 노력이 드는지에 대한 균형 문제가 존재한다.

UCS에 가깝고 true cost에서 멀어질수록, 더 적은 정보가 제공되는 휴리스틱을 의미한다.
이 경우, 휴리스틱 함수 자체를 계산하는데 드는 시간이 거의 없어 work per node는 작다.
하지만, quality of estimate도 낮아 탐색의 방향을 제대로 제시하지 못해 UCS처럼 거의 모든 방향으로 노드 확장해야 해 탐색할 노드 수를 폭발적으로 증가시켜 알고리즘의 시간 효율성을 떨어뜨린다.

true cost에 가깝고 USC에서 멀어질수록, 더 많은 정보가 제공되며 현실에 가까운 휴리스틱을 의미한다.
이 경우엔, 정확한 정보로 인해 quality of estimate는 높은 편이다. 하지만, work per node도 많아져서, 휴리스틱 함수 자체의 계산이 매우 복잡해지고 오래 걸린다.

즉, 적은 정보를 가진 휴리스틱 함수를 설계한다면 goal 탐색의 결과에 대한 문제가 생기고, 많은 정보를 가진 휴리스틱 함수를 설계한다면 노드당 작업량이 많아지면서 함수 계산이 복잡해진다.

따라서, 균형이 핵심이다.

5. Graph Search

같은 state들이 반복되기 때문에, 기존 tree search는 exponential하게 작업량이 늘어남
repeated node들의 확장을 막기 위해서 A* graph search 등장

A* Tree Search에 확장된 노드들의 집합(이때, closed set 이어야 함)을 통해 구현하고,
프론티어가 확장되긴 하는데, 노드를 확장하기 전에 이전에 확장했던 노드였는지를 판단해야 한다.
만약 새로운 노드가 아니면 그냥 skip하고, 새로운 노드라면 closed set에 추가한다.
closed set은 리스트가 아닌 set(집합)으로 구현한다.(중복도 없고 계산 비용도 더 낮다)
추가로, 반드시 방문했던 노드 중 cheapest cost에 대한 정보도 추적하고 있어야 한다.(optimal solution을 찾아야 하기 때문)
그래프 기반이기에 실제 구현은 딕셔너리를 활용한다.
[수도코드]

function A*-GRAPH-SEARCH(problem, frontier) return a solution or failure
  reached <- an empty dict mapping nodes to the cost to each one  
  frontier <- INSERT((MAKE-NODE(INITIAL-STATE[problem]), 0), frontier)  
  while not IS-EMPTY(frontier) do
    node, node.CostToNode <- POP(frontier)
    if problem.IS-GOAL(node.STATE) then return node
    if node.STATE is not in reached or reached[node.STATE] > node.CostToNode then
      reached[node.STATE] = node.CostToNode
      for each child-node in EXPAND(problem, node) do
        frontier <- INSERT((child-node, child-node.COST + CostToNode), frontier)
  return failure  

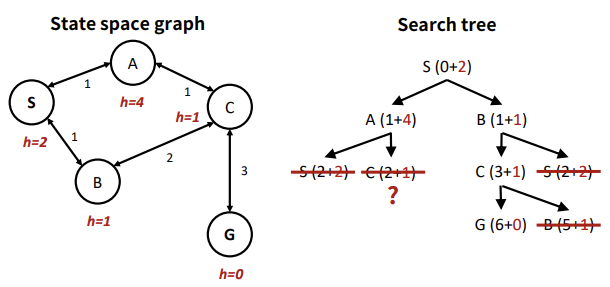
위 예시로 살펴볼 때, 이미 방문한 노드가 진짜 cheapest cost를 보장하는지를 판단하지 않는다면,
S->B->C 도달 후에, 바로 G로 간다. 즉, S->A->C가 더 optimal한 탐색임에도 불구하고 최적해를 따라가지 못하는 상황이 발생한다.
즉, f값이 A->C로 갈 때 감소하고, 이는 휴리스틱이 일관성이 없음을 의미하며, 더 좋은 휴리스틱을 설계하여 이러한 문제를 방지하여야 한다.

solution: Consistency of Heuristics

일관성(Consistency): 어떤 노드 A에서 C로 갈 때, A의 휴리스틱 값은 A에서 C로 가는 실제 비용과 C의 휴리스틱 값의 합보다 작거나 같아야 한다는 조건
수식으로 정리하면 다음과 같다.
\(h(A) \geq cost(A to C) + h(C)\)
이는 휴리스틱 값이 경로를 따라 갑작스럽게 크게 변하지 않고 실제 비용을 잘 반영한다는 의미

휴리스틱이 위와 같은 일관성을 만족하면, 경로를 따라 f값이 절대 감소하지 않음
\(h(A) - h(C) \geq cost(A to C)\)

A* tree search는 admissibility만 보장해도 최적성이 보장되지만,
A* graph search는 조금 더 타이트한 조건인 consistency가 보장되어야 중복 탐색을 피하면서도 최적해를 보장할 수 있다.

6. Conclusion

정리하자면, A* search는 backward cost와 forward cost를 동시에 고려한 탐색 기법이며, admissible하고 consistent한 휴리스틱 함수를 가지고 있다면, optimal한 해를 도출한다. 이때, 휴리스틱 설계가 핵심이다.