Post

[Artificial Intelligence] 03. Search (3): adversarial search

두 개 이상의 에이전트가 서로 적대적인 관계를 가정하고 탐색하는 문제에 대해서 다룹니다.

Posted Updated
alpha-beta pruning
alpha-beta pruning
By Youngbeom Cho
views 18 min read

1. Types of Games

인공지능이 다루는 다양한 게임들이 있고, 이를 아래와 같은 기준들(Axes)로 구분할 수 있음

  • Deterministic or Stochastic
  • Player 수
  • 제로섬 게임인지? (한 플레이어의 이득이 다른 플레이어의 손실과 정확히 일치하는 게임)
  • 완전 정보인지? (바둑처럼 모든 정보를 알고 있는지, 아니면 포커처럼 일부 정보가 가려져 있는지)

이렇게 다양한 게임들 속에서도 목표는 한 가지
각 state 에서 적절한 움직임을 결정하는 strategy(=policy)를 달성하기 위한 알고리즘을 찾는 것

Deterministic Games(결정론적 게임)

이 포스트에서 다룰 부분은 결정론적 게임으로,
다음과 같은 구성요소를 가진다.

  • States: S (+ start state $s_0$)
  • Players: $P = {1, 2, \dots, N }$ (일반적으로 턴제)
  • Actions: A (플레이어 의존적 혹은 state 의존적)
  • Transitions: $S \times A \rightarrow S$
  • Utilities: $S \times P \rightarrow R$ (특정 플레이어가 가지는 특정 상태가 그 플레이어에게 얼마나 유리한지를 나타낸 실수 값)
  • Goal test: $S \rightarrow {T, F}$

Goal: Policy ($S \rightarrow A$)를 가지는 플레이어에 대한 해를 찾는 것

Zero-Sum Games(제로섬 게임)

에이전트들은 서로 반대되는 유틸리티를 가지며, 한 에이전트가 유틸리티를 최대화하려고 한다면, 다른 에이전트는 유틸리티를 최소화하려 한다.

Game Tree

single-agent-game-tree
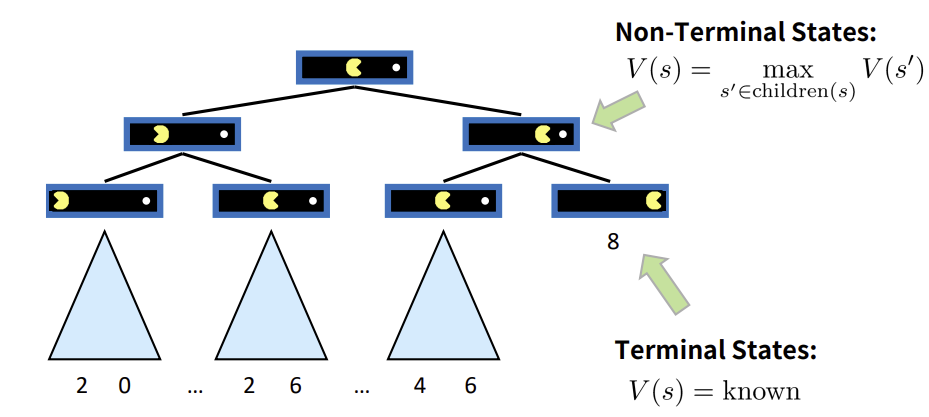
우선, 위와 같은 single-agent에 대한 game tree를 생각해보자.
혼자 플레이하는 게임의 모든 가능한 진행 경로를 트리 구조로 나타낸 것이다.
각 노드는 게임의 각 상태를 나타내며, edge(간선)은 에이전트의 action을 의미한다.
terminal nodes는 게임이 끝나는 최종 상태를 나타내며, 각 terminal nodes는 결과에 대한 명확한 점수(=유틸리티)를 가진다.
이때의 목표는 최상의 결과를 기준으로 판단하며, 가장 높은 최종 점수(유틸리티)를 얻는 것이다.

Value of a state: V(s)
non-terminal states (트리 상의 internal nodes, value of a state) => 자식 노드들의 V(s) 중 가장 큰 값을 취한다.
terminal states(=utility): utilities에 따라 계산한 알려진 값을 취한다.

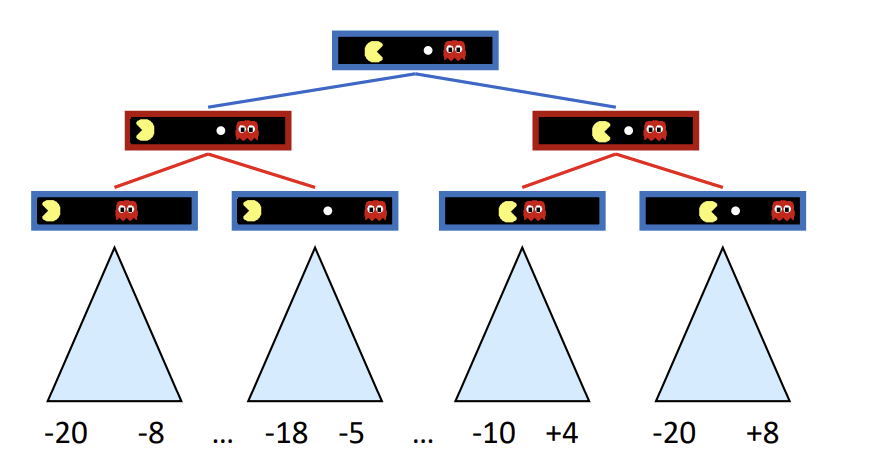
adversarial game tree
위처럼 적대적 게임인 경우, 상대 에이전트는 플레이어의 유틸리티를 최소화하려고 할 것, 이때 state value를 구하는 방법? => Minimax Value
적대적 게임의 간단한 특성을 활용한다.
에이전트는 유틸리티를 최대화하려 할 것이고, 반대로 상대 에이전트는 유틸리티를 최소화하려 할 것이다.
따라서, agent’s control을 받은 state들에는 successor(후임 노드)에서 max 값을 취하고, opponent’s control을 받는 state들에는 successor에서 min 값을 취한다.
위 예시의 경우 빨간색 opponent’s control을 받는 state에서는 왼쪽은 -8, 오른쪽은 -10을 취하게 될 것이며,
이에 따라 루트 노드인 start state는 -8을 state value로 취한다.

Deterministic하고, 제로섬 게임을 가정한다.
eg. 틱택토, 체스, 오목(Go)
한 플레이어는 결과를 최대화하려하고, 상대 플레이어는 결과를 최소화하려 한다.
각 플레이어는 차례를 번갈아 가진다.

Minimax Search
state-space search tree로 나타낸다.
합리적인(=optimal) adversary를 가정하고, 그에 대항하는 가장 좋은 성취 가능한 유틸리티인 각 노드의 minimax 값을 계산한다.

구현

1
2
3
4
5

def max_value(state):
    initialize v = - ∞  
    for each successor of state:
        v = max(v, min_value(successor))
    return v

1
2
3
4
5

def min_value(state):
    initialize v = + ∞
    for each successor of state:
        v = min(v, max_value(successor))
    return v

1
2
3
4
5
6
7

def value(state):
    if the state is terminal:
        return the utility
    if the next agent is MAX:
        return max_value(state)
    if the next agent is MIN:
        return min_value(state)

3. Improving the efficiency of Minimax: Alpha-Beta Pruning

Minimax의 Efficiency: exhaustive DFS와 같다.
시간복잡도: $O(b^m)$
공간복잡도: $O(bm)$
=> 거의 infeasible 함

불필요한 탐색 부분을 줄이기 위해 Alpha-Beta pruning을 도입
Search Tree에서 부분적으로 남아있는 children node를 α, β 값을 기준으로 skip하고, 탐색하지 않는 방식이다.

α: MAX 플레이어(agent, 나)가 현재까지 찾은 최선의 값(가장 높은 점수). 즉, 최소 확보한 점수를 의미
β: MIN 플레이어(Adversary, 상대방)이 현재까지 찾은 최선의 값(가장 낮은 점수). 즉, 최대 이 점수 이하로 막을 수 있다는 의미

MIN 노드에서 탐색 중인 노드의 값 v이 α보다 작거나 같아지면, 나머지 탐색 중단(어차피 MAX가 해당 경로 선택 X)
MAX 노드에서 탐색 중인 노드의 값 v이 β보다 크거나 같아지면, 나머지 탐색 중단(어차피 MIN이 해당 경로 선택 X)

특징

  • root에 대해 계산되는 minimax value에 영향을 끼치지 않음(= 최종 결과값이 안 바뀜)
  • 물론 중간 노드들의 값은 정확하지 않을 수도 있음
  • 자식 노드들이 잘 정렬되어 있으면 더 효과적인 pruning이 가능함
    => perfect ordering이면 $O(b^{m/2})$의 시간 복잡도로 감소, 탐색 깊이가 2배 증가

하지만, 여전히 체스같은 방대한 게임 완전 탐색 불가능

1
2
3
4
5
6
7
8
9

def value(state, α, β):
    if the state is root:
        initialize α = -∞, β = +∞
    if the state is terminal:
        return the utility
    if the next agent is MAX:
        return max_value(state, α, β)
    if the next agent is MIN:
        return min_value(state, α, β)

1
2
3
4
5
6
7

def max_value(state, α, β):
    initialize v = -∞
    for each successor of state:
        v = max(v, value(successor, α, β))
        if v >= β return v
        α = max(α, v)
    return v

1
2
3
4
5
6
7

def min_value(state, α, β):
    initialize v = +∞
    for each successor of state:
        v = min(v, value(successor, α, β))
        if v <= α return v
        β = min(β, v)
    return v

4. Depth-limited search & Evaluation function

Minimax Search와 alpha-beta pruning으로도 한계점이 존재해서,
실제 게임에선 Depth-limited search를 주로 활용
미리 정해 높은 깊이까지만 탐색하는데, terminal node에 도달하지 못했으므로, utility가 존재하지 않는다. 따라서, evaluation function을 통해 terminal position이 아닌 곳까지만 탐색한 값들로 얼마나 유리한지를 추정하는 과정이 필요하다.

어떤 Evaluation function을 써야 할까?
일반적으로 가중치를 적용한 피쳐들의 선형 합 형태로 계산한다.
\(Eval(s) = w_1 \cdot f_1(s) + w_2 \cdot f_2(s) + \cdots + w_n \cdot f_n(s)\)

하지만, 팩맨 예제를 통해서 살펴볼 때, 지금까지 쌓인 점수를 평가 함수로, depth-limit는 2로 설정하고 탐색했을 때, 팩맨이 굶어 죽는 문제가 발생하는데, 2수 앞 밖에 못 보는데 평가 함수 자체가 근시안적이기 때문에 의미 없는 행동을 반복하다가 결국 게임이 끝난다.
이를 해결하기 위해선, 가장 가까운 펠렛까지의 거리나 남아있는 펠렛의 개수 등으로 새로운 평가 함수를 작성하면 ‘펠렛’을 목표로 하는 피쳐가 새로 생겨나 유틸리티의 기대치를 반영할 수 있다.

어느 정도 깊이까지 탐색해야 좋을까?
Evaluation function은 항상 불완전하다.
이때 깊은 탐색이 평가 함수의 단점을 보완한다.
평가 함수가 복잡해지면, 정확해지지만, 깊은 탐색을 가져가기 힘들고,
평가 함수가 단순해지면, 부정확해지지만, 깊은 탐색을 가져갈 수 있다.

정리

Minimax Search는 완벽한, 최적의 상대방을 가정한 탐색이다.

하지만, 상대 에이전트가 항상 최적의 선택을 하지 못한다면?
=> 후술할 Expectimax Search가 이와 관련한 탐색 문제이다.

상대방이 최적이 아닌, 확률적으로 움직이는 것을 기대하는 탐색
주사위처럼 명시적인 무작위성, 예측 불가능한 상대, 로봇 바퀴 미끄러짐 같은 행동의 실패로 인해 항상 불확실성이 존재하는 현실의 게임을 반영한 탐색 방식
따라서, 최악의 경우를 대비하는 것이 아닌, 가능한 모든 결과의 average-case outcomes(평균적인 기댓값)을 계산하여, 그 기댓값이 가장 높은 선택을 하는 것이 합리적이다.
=> 구현은 chance node 도입을 톻애, 각 결과가 나올 확률을 통해 expected utilities를 계산하여 구하도록 한다. (일반적으로 weighted average, 가중 평균을 통해 계산한다)

1
2
3
4
5
6
7

def value(state):
    if the state is terminal:
        return the utility
    if the next agent is MAX:
        return max_value(state)
    if the next agent is EXP:
        return exp_value(state)

1
2
3
4
5

def max_value(state):
    initialize v = -∞
    for each successor of state:
        v = max(v, value(successor))
    return v

1
2
3
4
5
6

def exp_value(state):
    initialize v = +∞
    for each successor of state:
        p = probability(successor)
        v += p * value(successor)
    return v

Expectimax Pruning
expectimax는 upper/lower bound가 존재하지 않기 때문에,
모든 가능한 결과의 평균으로 결정되기 때문에 pruning의 기본 전제에 맞지 않아 쓸모가 없다.
Depth-limited Expectimax
현실 게임에선 게임 트리의 끝까지 탐색하는 것이 불가능하기에, 깊이 제한 탐색을 하고, 평가 함수를 통해 실제 expectimax value의 추정치를 구한다.
Modeling Assumptions
Minimax는 상대방이 optimal할 것을 가정해, worst-case를 대비하도록 설계된 전략
Expectimax는 상대방이 완벽하지 않은 기대(확률)에 따라 움직이는 존재로 가정해, average-case를 대비하도록 설계된 전략

Dangers of Optimism vs. Pessimism
당연하게도 Expectimax를 수행할 때, 상대방이 너무 적대적이고, optimal 할 것이라고 가정하는 것도 위험하고, 상대방이 너무 적대적이지 않을 거라고 가정하는(즉, worst-case 확률이 굉장히 적을 것이라고 가정) pessimistic한 가정도 위험하다.

6. Other games & Utility

zero-sum game이 아니거나 복수의 플레이어를 가정할 수 있는데, 이때 minimax의 일반화를 하면, terminal 노드는 utility tuples를 가진다. 중간 노드들도 튜플 형태로 나타나며 각 플레이어가 고유하게 가지는 인덱스 부분의 값으로 서로 자신의 utility를 계산하고 최대화 하려한다.

Utility

유틸리티란 게임의 특정 결과(world states)가 에이전트에게 얼마나 좋은지를 나타내는 실수
에이전트의 선호도나 목표 달성 정도를 정량적으로 표현한 값이다.

왜 minimax 대신 expectimax를 사용해야 할까?
결론부터 말하면, MEU(Principle of Maximum Expected Utility, 최대 기대 유틸리티 원칙) 때문이다.
MEU란, 합리적인 에이전트는 불확실한 상황속에서 자신의 지식을 바탕으로 기대 유틸리티를 최대화하는 행동을 선택해야 한다는 원칙이다.
폰 노이만과 모르겐슈테른의 정리에 따르면, 합리적 선호를 가진 에이전트의 선택은 항상 특정 유틸리티 함수 U로 표현되며, 이 함수는 각 결과의 유틸리티에 확률을 곱합 값의 합으로 계산된다.

돈과 관련한 인간의 유틸리티
돈 자체가 utility function으로 쓰일 순 없다.
일반적으로, 돈을 가졌을 때의 효용. 즉, 이를 돈의 utility로 다룬다.
대부분의 사람들은 위험을 회피하는 risk-averse 성향을 가진다.
이 때문에, 대부분 절반의 확률로 2억 받기보다 100프로의 확률도 1억 받기를 선호한다. (하지만 절박한 상황의 사람들은 위험 선호적 risk-prone 성향을 보이기도 한다.)

알레의 역설
인간의 유틸리티는 단순히 기댓값으로 결정되는 것이 아닌, ‘확실성’과 같은 심리적 요인에 의해 크게 변함을 보여주는 역설이다.

선택 1)

  • 100% 확률로 30억 받기
  • 80% 확률로 40억 받기

전자를 선택한다.(risk-averse)

선택 2)

  • 20% 확률로 40억 받기
  • 25% 확률로 30억 받기

후자를 선택한다.(더 큰 금액 노림)

Computer Science, Reinforcement Learning
adversarial search alpha-beta pruning minimax expectimax
This post is licensed under CC BY 4.0 by the author.