Automata 01: About Automata Theory & Basic Concepts
오토마타에 대해서 배우기 전, ‘집합론과 함수’, ‘자료구조(그래프이론 및 트리구조에 대한 이해)’, ‘귀류법 및 귀납법’ 에 대한 사전 지식이 필요합니다.
1. Automata Theory란?
오토마타 이론은 계산 능력이 있는 추상 기계와 그 기계를 통해 풀 수 있는 문제들을 연구하는 분야입니다.
여기서 오토마타(Automata)는 Automaton은 복수형으로, 계산 능력이 있는 자동화된 추상 기계, 수학적 기계를 의미합니다.
Wikipedia에 따르면, “대상의 어떤 기능에 주목하여 입력과 내부 출력 각 신호의 상호관계를 수학 모델로 옮기고, 이 모델을 수학적으로 고찰하여 결론을 유도하는, 내린 결론은 원래 대상에 맞는 다른 문제들을 해석하는 과정에 관여할 수 있도록 하는 학문”이라고 표현할 수 있습니다.
컴파일러, 인공지능, 컴퓨팅 이론, 컴퓨터 구조 설계 등 다양한 분야에 이용되는 이론입니다.
오토마타를 이해하기 위해선 컴퓨팅 이론에서의 3가지 중요한 개념에 대해 알아볼 필요가 있습니다. 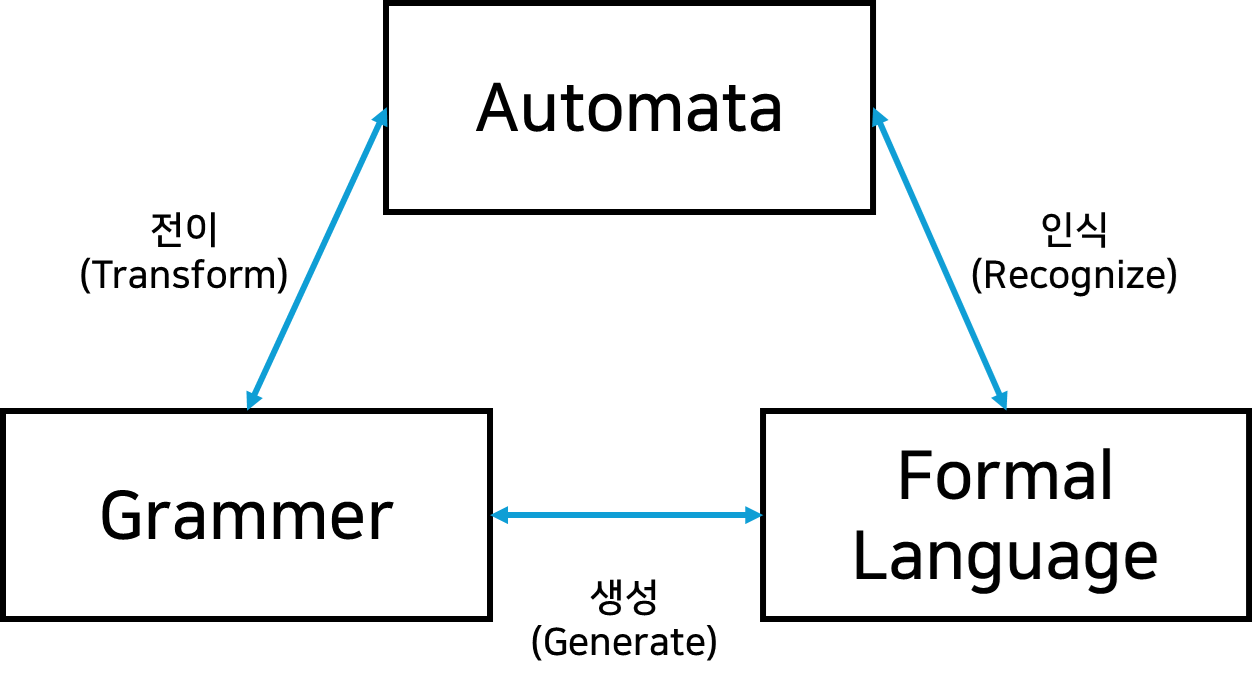
2. Computation Theory 3요소
Automata (오토마타)
디지털 컴퓨터의 추상적 모델을 의미합니다.
Formal Language (형식 언어)
심볼(Symbol)의 집합으로 구성된 알파벳(alphabet)으로 구성된 문자열의 집합을 의미합니다.
예를 들어, 기계어의 경우, {01, 0011, 000111, …}이 해당한다고 볼 수 있습니다.
Automaton M이 언어 L의 집합 원소를 모두 포함할 때,Automaton M이 언어 L을 인식한다고 표현합니다.Grammer (문법)
형식 언어를 정의하는 매커니즘입니다.
문법의 규칙 집합들을 기반으로 형식 언어가 생성됩니다.
3. (Formal) Language의 구성 요소
앞으로는 형식 언어(Formal Language)를 줄여서 그냥 언어라고 표현하겠습니다.
언어를 이해하기 위해서는 아래 세 가지 요소들을 살펴봐야 합니다.
Symbol(심볼)
언어를 이루는 가장 기본적인 요소입니다. 예를 들어, 한글의 자음&모음, 영어의 알파벳 문자, 0~9까지의 숫자 등을 생각하시면 됩니다.
예를 들어, 이진 알파벳 체계에서 0은 Symbol이며, 1도 Symbol 입니다.Alphabet(알파벳, $\Sigma$)
심볼의 공집합이 아닌 집합입니다. 유한해야 합니다.
예를 들면,
binary alphabet으로 {0, 1};
English alphabet으로 {a, …, z};
한글의 자음을 alphabet으로 {ㄱ, ㄴ, ㄷ, …, ㅎ};
생각해볼 수 있습니다.알파벳은 $\Sigma$ 기호로 표현합니다.
예를 들어, 0과 1로 이뤄진 이진 알파벳은 수식(1)과 같이 표현합니다.
\(\begin{align} \Sigma = \{0, 1\} \end{align}\)
예를 들어, a~z로 이뤄진 알파벳은 수식(2)과 같이 표현합니다.
\(\begin{align} \Sigma = \{a, b, \cdots , z \} \end{align}\)String(문자열)
문자열은 알파벳(<- 집합) 기반의 심볼들의 유한한 길이의 시퀀스(배열)입니다.
정의만으로는 이해가 어려우니 예를 들어 설명하겠습니다.위 수식(2)와 같은 알파벳이 있다고 가정할 때, “abc”나 “zero”는 $\Sigma = \{a, b, \cdots , z \}$에 대한 string입니다.
$\omega$, $\upsilon$ 등의 문자로 나타냅니다.
String의 연산
$a_1$, $a_2$, .. 라는
symbol, $\omega$, $\upsilon$ 이라는string이 있다고 가정할 때, 다음 연산들을 정의합니다.1) Concatenation
\(\displaylines { \omega = a_1a_2 \cdots a_n, \quad \upsilon = b_1b_2 \cdots b_n \\\ \omega\upsilon = a_1a_2 \cdots a_nb_1b_2 \cdots b_n }\)2) Reverse
\(\omega^R = a_N \cdots a_2a_1\)
쉽게 abc->cba와 같은 경우를 떠올리면 됩니다.3) Length
string $\omega$가 있을 때, $\omega$의 길이는 $|\omega|$로 표현합니다.
아래 수식 (3)의 성질 또한 만족합니다.
\(\begin{align} |\omega\upsilon| = |\omega| + |\upsilon| \end{align}\)4) Empty String
Empty string(빈 문자열)은 어떠한 symbol도 없는 문자열을 말하며, $\lambda$로 표현합니다.
아래 수식 (4), (5)의 성질을 만족합니다.
\(\begin{align} |\lambda| = 0 \newline \lambda\omega = \omega\lambda = \omega \end{align}\)5) Substring과 prefix/suffix
$\omega = \upsilon u$를 만족할 때, $\upsilon$과 $u$를 $\omega$의 substring(부문자열)이라고 표현합니다.
$\upsilon$은 $u$의prefix, $u$는 $\upsilon$의suffix라고 표현합니다.6) Repeat
다음은 문자열의 반복을 나타낸 여러 수식들입니다.
\(\displaylines{ \omega = \omega\omega\omega \cdots \omega\omega (n symbols) \\\ \omega^0 = \lambda \\\ a^2b^3 = aabbb \\\ |a^ib^jc^k| = i + j + k \\\ (ab)^2 = abab \\\ |x^k| = k|x| }\)7) Start-closure & Positive-closure
알파벳 $\Sigma = \{a, b\}$를 가정할 때,
$\Sigma$로 만들 수 있는 모든 문자열의 무한집합을 $\Sigma^*$로 표현하며, 이를 start-clousre라고 합니다. \(\begin{align} \Sigma^* = \{\lambda, a, b, aa, ab, ba, bb, aaa, aab, \cdots \} \end{align}\)
Positive-closure는 start-closure에서 빈 문자열($\lambda$)를 제외한 무한집합을 말합니다.
\(\begin{align} \Sigma^+ = \Sigma^* - \{\lambda\} = \{a, b, aa, ab, ba, bb, aaa, aab, \cdots \} \end{align}\)Language(언어)
언어는 일반적으로 start-closure($\Sigma^*$)의 부분집합으로 정의합니다.
어떤 언어 L에 포함되는 string을 L의 문장(Sentence)라고 표현합니다.
언어에도 마찬가지로 앞서 설명한 연산방식들이 동일한 방식으로 적용됩니다.1) Complement(언어의 여집합)
\(\bar{L} = \Sigma^* - L\)2) Reverse(언어의 역)
\(L^R = \{\omega^R: \omega \in L\}\)3) Concatenation(언어의 접합, 연결)
\(L_1L_2 = \{xy: x \in L_1, y \in L_2 \}\)
\(L^n = LL ... L\)
\(L^0 = \{\lambda\}\)4) Star-closure
\(L^* = L^0 \cup L^1 \cup L^2 ...\)
L의 문장들의 접합(concat)으로 구성할 수 있는 문자열의 집합입니다.5) Positive-closure
\(L^+ = L^1 \cup L^2 \cup ...\)
4. Grammer(문법)
저의 경우엔 문법을 이해하는 게 처음엔 많이 어려웠습니다. 생소한 부분이 많다 보니 어려울 수 있습니다. 하지만, 정의 그대로 이해하시고 예시를 적용하시다 보면 깨달음이 오는 순간이 오실겁니다!
문법은 언어(Language)에 의해 정의된 일정한 규칙을 기반으로 한 시스템입니다.
1) 문법 G의 정의
\(G = (V, T, S, P)\)