[Cryptography] 01.Introduction to Information Security & Cryptography

세줄요약

1. Information Security

Definition of Information Security

Information Security(정보 보호)는 Computer Security라고도 정의를 하며,
NIST95에 따르면 정보 시스템 리소스(-> HW, SW, Firmware, Infromation/Data, Telecommunication)의 다음 세 가지 특성을 모두 보호하는 목표를 달성하는 것으로 정의한다.

1. Confidentiality(기밀성)
2. Intergrity(무결성)
3. Availability(가용성)

위 세 가지를 CIA Triad라고 부른다.
이외에도 Authenticity(확실성), Accountability(설명가능성) 특성을 이야기하기도 한다.

Security Terminology

1. Adversary(=Threat Agent)
   시스템에 공격을 하는 주체
2. Attack
   지능적 위협을 통해 시스템 보안에 공격을 가하는 행위
3. Countermeasure
   위협, 취약점, 공격 등을 줄이기 위한 행동, 기기, 절차, 기술 등
4. Risk
   위험, 특정 위협이 특정한 해로운 결과를 만드는 취약점을 악용할 것이라는 가능성으로 표현되는 손실에 대한 기댓값
5. Security Policy
   시스템이나 기관이 민감하거나 중요한 자산을 보호하는 보안 서비스를 제공하는 방식을 구체화하거나 규제하는 규칙 또는 관행
6. System Resource(=Asset)
   자산, 정보 시스템에서 얻을 수 있는 데이터 혹은 시스템에서 제공하는 서비스 등
7. Threat
   위협, 잠재적인 보안의 위반
8. Vulnerability
   취약점, 시스템의 디자인(설계), 구현, 연산, 관리 등에서 약한 부분

Types of Vulnerability, Attacks & Countermeasure

1. Vulnerability
   • Corrupted
     무결성을 깨는 방식
   • Leaky
     기밀성을 깨는 방식
   • Unavailable or very slow
     가용성을 깨는 방식(e.g. DDoS)
2. Attacks
   • Passive vs. Active
   • Insider vs. Outsider
3. Countermeasure
   • Prevent
   • Detect
   • Recover

Fundamental Security Design Principles

• Economy of mechanism
• Fail-Safe defaults
• Complete mediation
• Open design
• Separation of privilege
• Least privilege
• Least common mechanism
• Psychological acceptability
• Isolation
• Encapsulation
• Modularity
• Layering
• Least astonishment

Attack Surfaces

시스템에서 도달할 수 있고 악용가능한 취약점이 존재하는 곳

• Network
• Software
• Human: 사회공학적 기법 등

Computer Security Strategy

• Security Policy
• Security implementation
• Security assurance
• Security evaluation

2. Introduction to Cryptography

초기는 안전한 communication을 위해서 암호가 작성되었다면,
현대에는 디지털 정보, 트랜젝션, 분산 컴퓨팅 등을 안전하게 하기 위한 기술로 사용되어지고 있다.

현대 암호학의 범위는 다음과 같다.

1. Primitives
   암호 시스템의 근간이 되는 함수나 알고리즘
   e.g. Hash function, random # generator 등
2. Schemes
   규격, 규정. Primitives의 집합.
   e.g. Encryption(암호화), Signature(서명) 등
3. Protocols
   둘 이상의 개체가 참여해 성립되는 암호 규약.
   e.g. Identification, Key establishment, Secret sharing 등
4. Cryptographic applications
   암호를 어플리케이션 단에서 사용하는 것
   e.g. Secure Internet Protocols(SSL, …), Electronic cash 등

Encryption(암호화)

데이터 기밀성을 제공하기 위한 기술

대칭키 암호화와 비대칭키 암호화 방식으로 나뉨

1. 대칭키 암호화
   • Block Cipher
   • Stream Cipher
2. 비대칭키 암호화
   • Factoring-based
     e.g. RSA
   • Discrete Logarithm-based
     e.g. ElGamal
   • PQC(Post-Quantum Cryptography): Lattice-based, Code-based, …
     e.g. NTRU

3가지 알고리즘을 따름

1. Setup Algorithm: Encryption의 초기 설정을 담당하는 필수적인 알고리즘. 매개변수를 바탕으로 암호화에 필요한 key와 복호화에 필요한 key를 생성하며,
   두 key는 대칭키의 경우 같으며, 공개키의 경우엔 다르다. 키 길이, 난수 생성 방식 등 전체 암호 시스템의 보안에 영향을 주기 때문에 얼마나 안전해야 하는지를 알 수 있는 알고리즘으로 볼 수도 있다.
   $\mathrm{Setup(\lambda)}$ -> $(K_{Enc}, K_{Dec})$
2. Encryption Algorithm: 암호화 키($K_{Enc}$)와, 평문(M)을 바탕으로, CT(Cipher Text, 암호문)을 생성한다.
   $\mathrm{Enc(}K_{Enc}, \mathrm{M)}$ -> $\mathrm{CT}$
3. Decryption Algorithm: 복호화 키($K_{Dex}$)와, 암호문(CT)를 바탕으로, 평문(M)을 생성한다.
   $\mathrm{Dec(}K_{Dec}, \mathrm{CT)}$ -> $\mathrm{M}$

Symmetric Encryption (=Private Key Encryption, Secret Key Encryption)

Sender와 Receiver가 모두 동일한 키를 가지고 있다는 것이 큰 특징

1. 주어진 Plain Text(M)을 비밀키 K를 통해 암호화하여 CT 생성
2. 생성된 CT를 바탕으로 비밀키 K를 통해 복호화하여 다시 평문(M)을 생성한다.

고전적인 암호화 기법
Block Cipher - DES, AES, ARIA, SEED
Stream Cipher - RC3, ChaCha

장점: 공개키 암호에 비해 빠름
단점: 키 공유를 미리 해야 하는 문제, 키가 많이 필요하다는 문제 => $\binom{N}{2}$ 개의 키 필요

Asymmetric Encryption (=Public Key Encryption)

암호화에 사용되는 키와 복호화에 사용되는 키가 다른 것이 큰 특징
암호화에는 Public Key(공개키)를 사용하며, 복호화에는 개인키(비밀키, Private Key, Secret Key)가 사용된다.

1. 평문을 Public Key를 통해 암호화하여 암호문을 만들고, Public Key를 통해 Secret Key(=개인키)를 만든다.
2. 암호문을 생성한 Secret Key를 바탕으로 복호화하여 평문을 얻는다.

RSA, ElGamal, NTRU 등이 있다.
장점: 키 공유가 비교적 쉽다. 키의 개수가 적기 때문에 키 관리가 용이하다.
단점: 대칭키 암호화에 비해 느리다. 아래 사진처럼 공개키 ring 뭉치로 관리하기 때문!

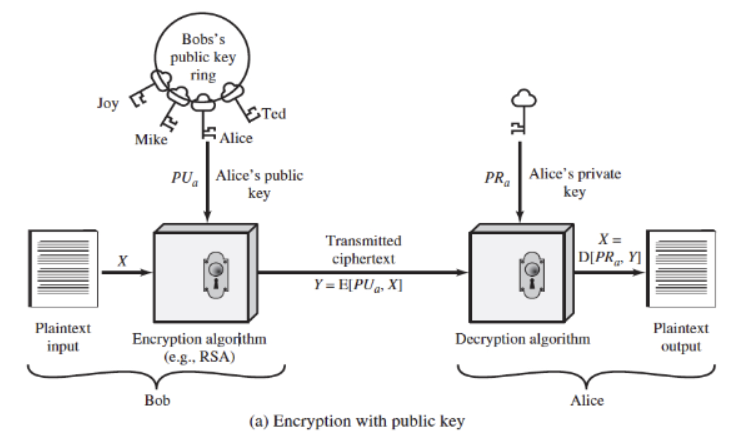
Terminology for Encryption

• Plaintext(평문): 암호 알고리즘에 input으로 주어지는 원본 메시지/데이터
• Ciphertext(암호문): 암호화 알고리즘의 output
• Encryption(암호화): 평문과 key를 input으로 가지고, 암호문(Ciphertext)를 반환하는 알고리즘
• Decryption(복호화): 암호문과 key를 input으로 가지고, 평문을 반환하는 알고리즘

Kerckhoff’s Principle

암/복호화 알고리즘은 비밀일 필요가 없다.(=숨길 필요가 없다.)
암/복호화 알고리즘은 불편함없이 공격자에 의해 일어날 수 있음에 틀림없다.
즉, 암호 시스템의 안전성은 암호 알고리즘의 기밀성이 의존해선 안 된다.
또한, 단순히 “비밀키”만 비밀로 유지하도록 가정하고, 나머지(공개키, 암호 알고리즘 등)의 경우는 공개되었다는 가정하에 암호에 대한 안전성을 따져야 한다.

Open Design을 채택한 원리라고도 할 수 있다.

왜 비밀키만 비밀이라는 점만 고려해 안전성을 따질까?
비밀이 최소화 되는 것은 비용을 최소화하는 것이기 때문이다.

• 알고리즘보다 비밀키를 드러나지 않게 유지하는 것이 더욱 쉽다.
• 만약 키가 유출되었다면 키만 바꾸면 된다.
  즉, Recover 상황을 가정했을 때, Key만 비밀로 유지하면, Key만 갈아 끼우면 되지만,
  암호 알고리즘도 비밀로 했을 때 암호 알고리즘이 유출되었다면 알고리즘 전체를 뜯어 고쳐야 되므로, 유지보수 비용이 증가하는 것이다.
• 다른 알고리즘을 사용해서 다른 사람들과 소통하는 것보다 다른 키를 사용해 소통하는 것이 더 효율적이고 쉽다.

이외에도 여러 가지 이유가 있지만 비슷한 이유이므로 생략.

Basic Types of Attacks against Encryption

1. Brute-force Attack: 타겟한 암호문에 대해서 모든 가능한 키를 일일이 대입/대조하는 공격, Encryption Scheme 설계 시 가장 우선적으로 고려하는 공격
   Key Size를 크게 만들면 어느 정도 해결이 가능하다.
2. Cryptanalysis(암호해독)
   공격자에게 주어진 정보와 그 범위에 따라 4 가지의 종류로 구분한다.
   1) Ciphertext Only
   공격자가 암호문만 가지고 평문을 유추하는 방식
   2) Known Plaintext
   공격자가 일부 평문과 이에 대응하는 암호문을 알고 있는 상황에서, 이를 이용해 다른 암호문을 해독하는 방식
   e.g. 앨런 튜링의 애니그마 해독
   3) Chosen Plaintext
   공격자가 특정 평문을 선택하여 암호화한 결과를 분석하여 공격하는 방식
   4) Chosen Ciphertext
   공격자가 특정 암호문을 선택하여 복호화한 결과를 분석하여 공격하는 방식

3. Classical Encryption

Preliminaries(Notations)

\(\mathbb{Z}_m = \{0, 1, 2, \dots, m-1\}\)
m으로 나눈 나머지 값에 대한 집합이다.

g mod p: 모듈로 연산으로, g를 p로 나눈 나머지를 말한다.
당연히 나머지는 0 이상인 정수이다.
e.g. -7 mod 26 = 19, 정수론의 합동식 표현으로는 $-7 \equiv 19 \quad (mod 26)$

Alphabet 문자만 사용하기 때문에 $\mathbb{Z}_{26}$에 속한 원소들에 a부터 z까지 차례대로 숫자로 대체하여 사용한다.

Shift Cipher(시프트 암호)

정의
For $0\leq K \leq 25$ ,
\(Enc(K, x) = (x+K) \; mod \; 26\)
\(Dec(K, Y) = (Y-K) \; mod \; 26\)

예시
if K = 9:
SHIFT (18 7 8 5 19)
각각 +9 한 뒤에 mod 26
BQROC (1 16 17 14 2)
복호화는 역으로 계산
각각 -9 한 뒤에 mod 26
SHIFT (18 7 8 5 19)

cf. K=3인 경우는 카이사르 암호에 해당한다.

공격/취약점

1. Private Key의 후보가 오로지 26개이기 때문에 Brute-force Attack에 취약함
2. Known Plaintext Attack에 취약하다.
   예를 들어, 평문 SHIFT가 BQROC로 암호화되는 상황이라면,
   B - S = (1 - 18) mod 26 = 9 = K
   $K=9$임을 쉽게 알 수 있다.

Affine Cipher(아핀 암호)

정의
$For \; K=(\alpha, \beta) \; where \; \alpha, \beta \in \mathbb{Z}_{26} \; and \; gcd(\alpha, 26) = 1$ ,
\(Enc(K, x) = \alpha x+\beta \; mod \; 26\)
\(Dec(K, Y) = \alpha^{-1}(Y-\beta) \; mod \; 26\)

예시
if $K=(\alpha, \beta)=(7, 3)$:
HOT (7 14 19) -> AXG (52 101 136)
7 => 77+3 mod 26 => $52 \equiv 0$ => A
14 => 147+3 mod 26 => $101 \equiv 23$ => X
19 => 19*7+3 mod 26 => $136 \equiv 6$ => G

그렇다면 복호화는?

A(0) -> $(0-3) \times 7^{-1}$
$-\frac{3}{7}$이 되는 것 같지만, 이런 형태로는 목표로 하는 정수값을 계산할 수 없다.
위 암호는 mod 26의 세계에서 동작하는 매커니즘이라는 아주 단순한 사실을 이해하면 쉽게 복호화할 수 있다.
$7^{-1}$ mod 26을 다른 표현으로 풀어나가면 된다.
즉, mod 26 베이스의 합동식에서 7의 모듈러 역원을 찾아가야 하며, 역으로 유클리드 호제법을 사용하면 구할 수 있다. => $7x \equiv 1 \quad (mod 26)$의 해를 구하는 과정
(cf. 유클리드 호제법이란 두 양의 정수 혹은 두 다항식의 최대공약수를 구하는 알고리즘이다.)

\[26 = 3 \times 7 + 5 \\ 7 = 1 \times 5 + 2 \\ 5 = 2 \times 2 + 1 \\ 2 = 1 \times 2 + 0\]

위와 같이 전개가 가능한데, 그렇다면 1을 기준으로 역으로 전개해보자. 1을 7과 26의 조합으로 표현하는 것을 목표로 한다.(왜냐면, gcd(7, 26)=1 이라는 특징을 알고 있기 때문이다.)

\[1 = 5 - 2 \times 2 \\ = 5 - 2 \times (7 - 5 \times 1) \\ = 3 \times 5 - 2 \times 7 \\ = 3 \times (26 - 3 \times 7) - 2 \times 7 \\ = 3 \times 26 - 11 \times 7\]

mod 26 세계에선 26의 배수는 전부 0으로 취급하기 때문에 $-11 \times 7 \equiv 1 \quad (mod 26)$으로 표현된다.
즉, 7 mod 26의 역원을 찾았는데, -11로 표현되므로 26을 더해 계산이 편하도록 15로써 역원을 작성한다.

따라서, $-3 \times 15 \quad (mod 26)$를 통해 A(0)의 복호화를 할 수 있게 된다.
따라서, $-45 = -26 \times 2 + 7$ 즉, $-45 \equiv 7$이므로, 7에 해당하는 H로 복호화가 가능한 것을 알 수 있다.

왜 $gcd(\alpha, 26) = 1$을 만족해야 하는가?
위 복호화 과정에서 알 수 있듯이, 해당 조건을 만족해야 모듈러 역원이 존재할 수 있기 때문이다. 즉, $\alpha$가 26과 공통되는 약수를 가지고 있으면 역원이 존재하지 않는다.

공격/취약점
가능한 $\alpha$값이 12개, $\beta$는 $\mathbb{Z}_{26}$ 상에 있으므로, 총 26개.
즉, 가능한 private key의 후보는 총 312개로, 비교적 적은 수이기 때문에 Brute-force attack에 취약하다.
뿐만 아니라, Known-plaintext attack에도 취약한데,
위의 예시를 이어서 설명하면, H가 A에 대응되고, O가 X에 대응되는 상황이기 때문에,
$\alpha$, $\beta$에 대한 합동 연립방정식이 나오게 되는데 어떻게든 풀릴 수 밖에 없다는 점에서 known-plaintext attack에 취약함을 알 수 있다.

Substitution Cipher(치환 암호)

정의
$For \; K=\pi \; where \; \pi \; is \; a \; permutation \; on \; \mathbb{Z}_{26}$
\(Enc(K, x) = \pi(x)\)
\(Dec(K, Y) = \pi^{-1}(Y)\)

예시
A -> S
B -> C
C -> F
$\vdots$
Z -> A
각각의 alphabet에 대하여 다른 alphabet으로 치환되는 함수 $\pi$가 존재한다고 가정하자.

AC를 암호화한다고 했을 때,
$\pi(A)\pi(C) = SF$와 같은 방식으로 암호화된다.

복호화의 경우, 마찬가지로 $\pi^{-1}$, 즉 $\pi$의 역함수를 적용시키면 된다.

Bit-string의 경우,
8개의 bit로 되어 있다고 했을 때, $2^8$개의 bit-string 경우의 수가 존재하기 때문에
$256!$ 개의 비밀키 후보가 존재한다.

공격/취약점
Brute-force attack의 경우, $26!$개의 private key 후보가 있있는데, 이는 $2^{88.3}$ 가량 되며, 브루트포스 공격을 막기에 충분한 비밀키이다.
하지만, Chosen-plaiontext에 취약한데, n개의 치환관계를 안다면 (26-n)!로, 기하급수적으로 비밀키의 후보가 감소하는 것을 확인할 수 있다.

cf. Statistical Test: 영어의 경우 평균적인 알파벳 사용빈도에 따라 암호문을 유추할 수 있다.(예를 들면, e가 가장 많이 나오기 때문에 빈도가 가장 높은 문자를 e로 설정하여 유추)

Vigenère Cipher(비제네르 암호)

정의
Key를 각 알파벳마다 다른 값을 적용시키는 방식
For $K=(k_1, \dots, k_m) \in (\mathbb{Z}_{26})^m$,
Enc($K, x_1, \dots, x_m$) = ($x_1+k_1, \dots, x_m+k_m$)
Dec($K, Y_1, \dots, Y_m$) = ($Y_1+k_1, \dots, Y_m+k_m$)

공격/취약점
Brute-force attack에 취약하다고 할 수도 있지만, key의 길이가 증가할수록 안전해진다.
$26^m$개의 private key 후보가 생긴다. 여기서 m은 key의 길이고, $26^{18}$만 되어도 $2^{84.6}$이기 때문에 브루트포스에 대해 비교적 안전해지는 상황이 된다.
Ciphertext only attack에 취약할 수 있는데, kasisiki test 같은 통계적 test 방식(알파벳이나 단어 출현 빈도에 따른 평문 예측)으로 풀릴 수 있다.
Known-plaintext attack에도 취약하다. 만약 m이 알려진다면.

Permutation Cipher(순열 암호)

정의
For a key $K = \pi$ where $\pi$ is a permutation of ${1, \dots, m}$
Enc($K, x_1, \dots, x_m$) = ($x_{\pi(1)}, \dots, x_{\pi(m)}$)
Dec($K, Y_1, \dots, Y_m$) = ($Y_{\pi(1)}, \dots, Y_{\pi(m)}$)

Index에 substitution(치환 함수)을 적용하는 방식, 순서를 섞는다.

\((x_1 \dots x_m)P = (Y_1 \dots Y_m)\)
위와 같이 행렬의 곱으로써 표현할 수도 있다.(P는 permutation matrix이다.)

공격/취약점
$m!$개의 private key 후보들이 있으며, m 값이 크면 brute-force attack에 안전하지만, m 값이 작으면 안전하지 않다.
Known-plaintext attack이나 Chosen-plaintext attack에 취약한데, 평문과 암호문에 대응되는 쌍을 많이 얻으면 역행렬을 곱해 $P^{-1}$을 얻을 수 있기 때문이다.

LFSR Cipher(Linear Feedback Shift Register 암호)

One-Time Pads