[DataStructure] 01. Introduction: Algorithms & ADT

Algorithm

A finite set of instructions that accomplish a particular task
특정 작업을 수행하는 명령어들의 유한한 집합

구성 요건: Input, Output, Definiteness, Finiteness, Effectiveness

대표적인 정렬 알고리즘을 살펴본다.

Selection Sort

Finds the smallest element and swaps it with the first element
가장 작은 원소를 찾고, 첫 번째 원소와 swap(자리바꿈) 한다.

void selectionSort(int arr[], int n) {
    int min_idx, tmp;
    for (int i=0; i<n-1; i++) {
        min_idx = i;
        for (int j=i+1; j<n; j++) {
            if (arr[j] < arr[min_idx]) {
                min_idx = j;
            }
        }
        tmp = arr[min_idx];
        arr[min_idx] = arr[i];
        arr[i] = tmp;
    }
}

Bubble Sort

Repeatedly swaps adjacent elements if they are in the wrong order
순서가 잘못되었으면, 인접한 원소와 반복해서 swap한다.

void bubbleSort(int arr[], int n) {
    int tmp, swapped;
    for (int i=0; i<n-1; i++){
        swapped = 0;
        for (int j=0; j<n-i-1; j++){
            if (arr[j] > arr[j+1]) {
                tmp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = tmp;
                swapped = 1;
            }
        }
        if(!swapped) break; // If no swaps, break early
    }
}

Insertion Sort

Inserts each element into its correct position
각 원소를 정확한 position에 삽입한다.

void insertionSort(int arr[], int n) {
    int key, j;
    for (int i=1; i<n; i++) {
        key = arr[i];
        j = i-1;
        while(j >= 0 && arr[j] > key) {
            arr[j+1] = arr[j];
            j--;
        }
        arr[j+1] = key;
    }
}

Merge Sort

Divides array, sorts subarrays, and merges them
배열을 나누고, 정렬한 다음, 병합한다.
```c void merge(int arr[], int left, int mid, int right) { int n1 = mid-left+1; int n2 = right-mid; int L[n1], R[n2];

for (int i=0; i<n1; i++) L[i] = arr[left+i];
for (int i=0; i<n2; i++) R[i] = arr[mid+1+i];

int i=0, j=0, k=left;

while (i < n1 && j < n2) {
    if (L[i] <= R[j]) arr[k++] = L[i++];
    else arr[k++] = R[j++];
}
while (i < n1) arr[k++] = L[i++];
while (j < n2) arr[k++] = R[j++]; }

void mergeSort(int arr[], int left, int right) { if (left < right) { int mid = (left + right) / 2; mergeSort(arr, left, mid); mergeSort(arr, mid+1, right); merge(arr, left, mid, right); } }

### Recursive Algorithm  
> An algorithm calls itself for subproblems  
> 작은 문제들을 해결하기 위해 알고리즘 자기 자신을 다시 호출하는 방식  

예) Fibonacci  
```c
int fibonacci_recursion(int n) {
	if (n == 0) return 0;
	if (n == 1) return 1;
	return fibonacci_recursion(n-1) + fibonacci_recursion(n-2);
}

장점

1. 알고리즘을 표현하기에 자연스럽다.
2. 코드를 작성하고 디버깅하는 데 필요한 시간이 줄어든다.

단점

1. 메모리 사용량이 높다.
2. iterative counterpart(반복문) 방식보다 시간 소요가 크다.

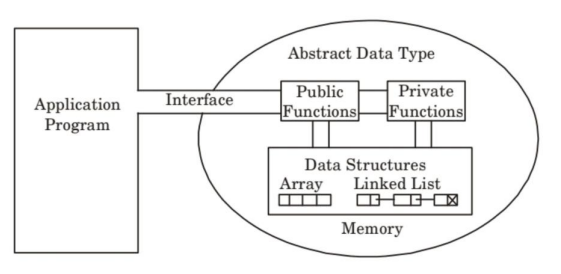
ADT (Abstract Data Type)

자료구조가 어떤 방식으로 구성되어 있는지에 기반해서 다른 연산을 수행하기를 원하지 않기 때문에, 구현 방식에 대해 명시하지 않고 자료구조의 특성과 operation만을 설명하는 형태.
대표적으로, 스택과 큐가 있음.

Performance Evaluation(-> 알고리즘(complexity 정리))

• Machine-dependent Measurement
  프로그램 실행 시간
  프로그램 실행하는 각각의 환경마다 다를 수 있음
• Machine-independent Analysis -> Asymptotic Analysis
  공간복잡도 & 시간복잡도

공간복잡도

입력 길이에 따라 알고리즘이 실행하는 데 차지하는 공간의 양

• Fixed Space
  프로그램의 input과 output 크기에 대한 숫자와 상관없이 차지하는 상수 공간
  e.g. memory for instructions, 상수, 정적 변수 등
• Variable Space
  프로그램의 input size에 의존하는 공간
  e.g. 재귀 스택으로 인한 메모리, 참조 변수 등

시간복잡도

입력 길이에 따라 알고리즘이 프로세스를 끝마치는데 소요되는 시간의 총 양

실행되는 primitive operation 또는 step의 개수

예제

int sum(int list[], int n){
	int i;
	int temp_sum = 0;
	for (i=0; i<n; i++) {
		temp_sum += list[i];
	}
	return temp_sum;
}

Fixed Space: 배열 포인터 list, 정수 n, 정수 i, 정수 temp_sum (=> 총 4*4 bytes)
Variable Space: 0

Time Complexity: 2+(n+1)+n+1 = 2n+4

int recursive_sum(int list[], int n){
	if (n)
		return (recursive_sum(list, n-1) + list[n-1]);
	return 0;
}

Fixed Space: 배열 포인터 list, 정수 n (=> 총 24 bytes)
Variable Space: 배열 포인터 list, 정수 n, return address (=> 34 bytes)

Time Complexity: (n+1)+n+1 = 2n+2