[FHE] 01. Mathematical Background & Cryptography

1. Cryptography

일반적으로 암호는 data confidentiality(기밀성)를 제공하기 위한 기술입니다.

기본적으로 사용되는 용어들을 정리합니다.

• 평문(Plaintext): 암호화되지 않은 원본 데이터
• 메시지(Message): (=평문)
• 키(Key): 암·복호화에 사용되는 정보
• 암호문(Ciphertext): 특정 암호화 알고리즘을 이용해 평문을 암호화한 데이터
• 스킴(Scheme): 암호 시스템 전체 설계 및 구성 요소의 집합 (eg. AES, RSA, Elgamal, …)
• 알고리즘(Algorithm): 암호 스킴 내에 특정 기능을 수행하는 구체적인 절차 (eg. 키 생성 알고리즘, 암·복호화 알고리즘)

일반적으로 암호 스킴은 사용하는 키의 성질에 따라 대칭키 암호와 공개키 암호로 분류됩니다.

1. 대칭키 암호: 암·복호화에 동일한 secret key(=private key)를 사용하는 암호 스킴입니다. (eg. AES)
   • Block cipher(블록 암호): 평문을 블록 단위로 쪼개 암호화합니다.
   • Stream cipher(스트림 암호): 평문이 들어오는대로 주어진 key에 대하여 pseudorandom number generator를 활용해 key stream을 생성하여 바로바로 암호화합니다.
   • SKE의 Correctness
     SKE는 아래와 같은 probabilistic polynomial-time 알고리즘 세 가지가 존재합니다.
     \(\text{KeyGen}(\lambda) \rightarrow sk\)
     \(\text{Enc}(sk, m) \rightarrow c\)
     \(\text{Dec}(sk, c) \rightarrow m'\)
     SKE의 Correctness는 위 알고리즘과 함께 다음과 같이 정의합니다.
     $\text{SKE} = (KeyGen, Enc, Dec)$이 correct하다는 의미는
     \(\text{Pr[Dec(}sk, \text{Enc}(sk, m)) \neq m]\)
     위 확률이 negligible하다는 의미입니다.
2. 공개키 암호: 비대칭키 암호라고도 하며, 암·복호화에 사용되는 키가 다릅니다. (eg. RSA)
   • PKE의 Correctness
     PKE도 마찬가지로 probabilistic polynomial-time 알고리즘 세 가지가 존재합니다.
     \(\text{KeyGen}(\lambda) \rightarrow (pk, sk)\)
     \(\text{Enc}(pk, m) \rightarrow c\)
     \(\text{Dec}(sk, c) \rightarrow m'\)
     SKE의 Correctness는 위 알고리즘과 함께 다음과 같이 정의합니다.
     $\text{SKE} = (KeyGen, Enc, Dec)$이 correct하다는 의미는
     \(\text{Pr[Dec(}sk, \text{Enc}(pk, m)) \neq m]\)
     위 확률이 negligible하다는 의미입니다.

공개키 암호의 경우, 아래와 같이 Security Model을 Security Game으로 정의할 수 있습니다.

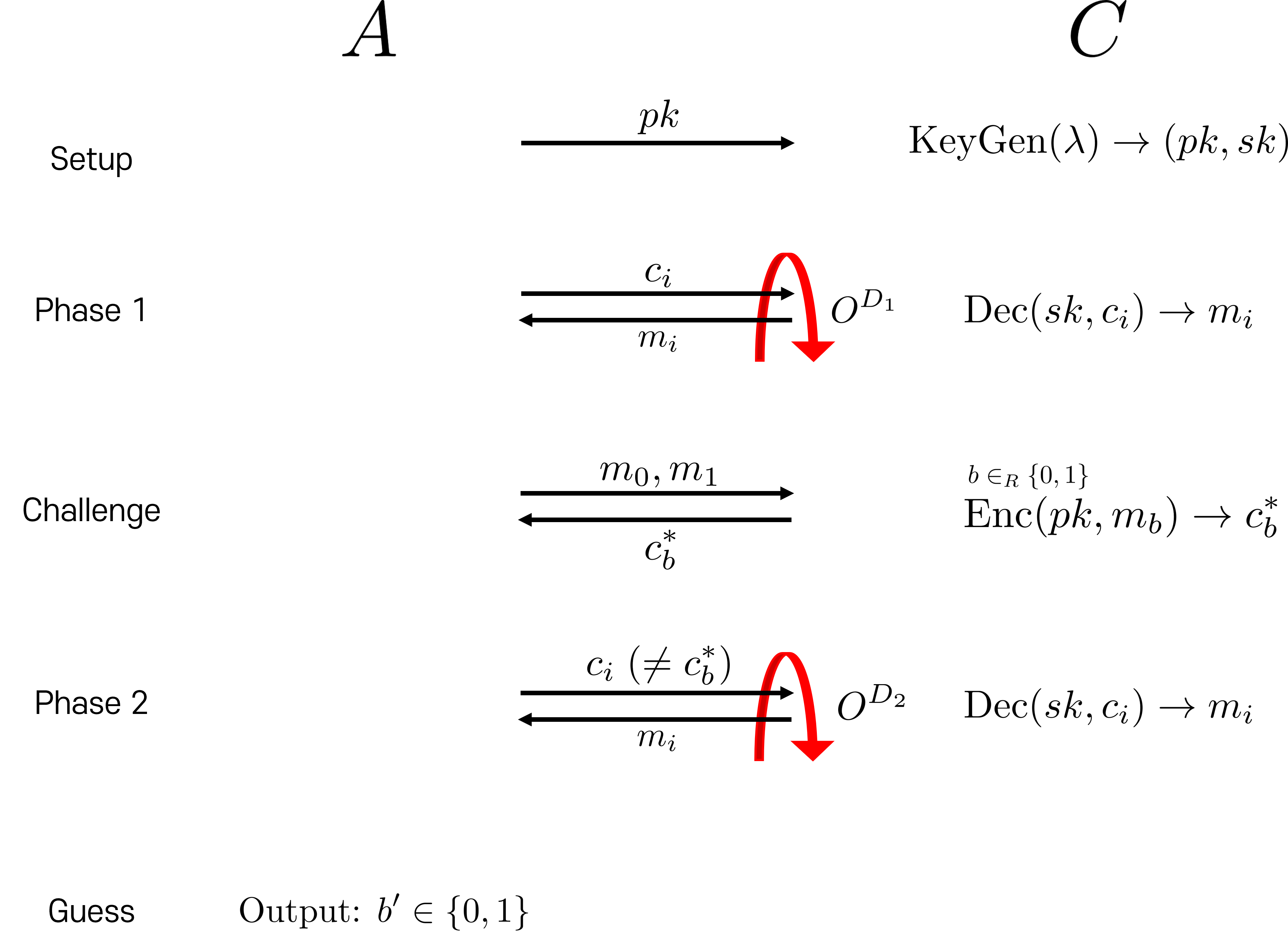
A는 Adversary(공격자)로, C는 그 공격을 막는 Challenger(챌린저, 도전자)를 설정합니다.

1. Guess: C는 키 생성 알고리즘을 통해 공개키와 비밀키를 생성하고, 공개키를 공격자(A)에게 건넵니다.
2. Phase 1: 공격자(A)는 Decryption Oracle($O^{D_1}$)에 암호문 $c_i$를 보내 C는 복호화 알고리즘을 통해 복호화하고, 공격자는 평문($m_i$)을 전달 받습니다. 이 복호화 시도는 polynomial(다항) 시간에 여러 차례 진행됩니다. 즉, Chosen Cipher Text Attack이 가능한 상황입니다.
3. Challenge: 공격자는 충분한 복호화 테스트를 하고, 동일한 길이의 평문 ($m_0$, $m_1$)을 C에게 보냅니다. C는 랜덤한 비트 (0, 1) 중 하나를 선택하여, 해당하는 평문을 암호화하고 다시 그 결과를 공격자(A)에게 보냅니다.
4. Phase 2: 공격자(A)는 받은 암호문이 아닌 여러 암호문들을 Decryption Oracle에 보내 복호화된 평문을 받을 수 있습니다.
5. Guess: 여러 차례의 CCA에 대하여 복호화된 평문을 받은 결과를 바탕으로, Challenge 단계에서 받았던 암호문이 $m_0$을 암호화한 결과인지, $m_1$을 암호화한 결과인지 추론합니다.

이때, A이 위 security game에서 의미있는 결과를 도출할 확률을 아래와 같이 정의합니다.
\(\text{Adv}^{\text{IND-XXX}}_{A,\,PKE}(\lambda) = |Pr[b = b']-\frac{1}{2}|\)
1/2을 빼는 이유는 찍어 맞출 확률 절반을 빼야 하기 때문이고, 절댓값을 씌우는 이유는 높은 확률로 못 맞히는 경우도 의미있는 결과를 도출하기 때문입니다. (나온 결과의 반대로 선택하면 됩니다.)

이때, probabilistic polynomial-times adversary인 A와 security parameter $\lambda$에 대하여 위 확률이 negligible한 경우를 IND-XXX에 대하여 secure하다고 이야기합니다.

• Probabilistic을 정의한 이유는, deterministic이 되면 안 되기 때문입니다. deterministic은 동일한 평문에 대하여 동일한 암호문으로 암호화, 동일한 암호문에 대하여 동일한 평문으로 복호화되는 암호 스킴을 말합니다. 이런 상황은 취약하기 때문에 일반적으로 salt값을 주어 probabilistic한 암호 스킴을 설계합니다.
• IND는 indistinguishable의 약자입니다. $m_0$, $m_1$이 구분 불가능한 상황이 안전하기 때문에, indistinguishable의 약자를 따옵니다.

1. IND-CCA2: Adversary는 Phase 1과 Phase 2의 Chosen Ciphertext Attack이 모두 가능하며, 이에 대하여 안전한 PKE Scheme을 말합니다.
2. IND-CCA1: Adversary는 Phase 1의 Chosen Ciphertext Attack만 가능하며, 이에 대하여 안전한 PKE Scheme을 말합니다.
3. IND-CPA: Adversary가 Challenge 단계만 가능한, Chosen Plaintext Attack만에 안전한 PKE Scheme을 말합니다.
   cf. IND-CPAD: Phase 2에서의 한 두차례 가량의 Decryption 질의가 가능한 security model입니다.

일반적으로, IND-CPA에 대해 안전한 스킴을 설계하는 것을 목표로 합니다.

2. Lattice-based Cryptography

현대 암호는 Lattice라는 수학적 구조를 기반으로 한 암호를 사용합니다.

3. Mathematical Background

Monoid vs Group vs Ring vs Field

우선, 항등원과 역원을 정의합니다.

• 항등원: $\forall x \in S, \; e * x = x$를 만족하는 $e$
• 역원: $\forall x \in S, \; x * a = e$를 만족하는 $x$

1. Monoid
2. Group
3. Ring
4. Field