[NLP] Attention Is All You Need
1. Abstract
기존: Recurrent or convolutional neural network 기반의 sequence transduction model
논문 제시: Attention Algorithm 기반의 Transformer (Recurrence나 Convolutions X)
제시한 이유 1) more parallelizable(더 병렬처리 성능이 좋음)
제시한 이유 2) less time to train(훈련 시간 더 줄음)
정당성 부여는 NLP Task에 대한 학습 및 성능 실험을 통해서 이뤄짐
정당성 부여 1 - English -> German 번역
정당성 부여 2 - English -> French 번역
2. Conclusion
- Attention 기반(multi-headed self-attention)의 Tranformer 모델의 개발로 기존 인코더-디코더 모델 대체
- 더 빠르게 훈련 가능
- text 이외의 input/output modality로 확장을 기대
cf. modality: 입력 데이터의 종류 또는 유형을 의미 - Make generation less sequential(덜 sequential한 Transformer)은 다음 목표
3. Introduction & Background
RNN, LSTM, GRN 등은 sequence modeling과 transduction problem에 대한 최신 접근 방식
cf. Inductive Learning vs. Transductive Learning
RNN 계열 모델(LSTM, GRN 포함)은 sequential computation의 한계인 parallelization 불가
Attention 매커니즘은 recurrent network(RNN 계열)에서 대부분 사용되었음
Transformer는 recurrence를 제외하고 입출력 간의 global dependency를 학습하기 위해 attention 매커니즘에 의존하는 모델 아키텍처
장점: 병렬 처리 + 12h동안 8개의 P100 GPU로 훈련해 최첨단 번역 품질 제공 (=> more parallelization & less cost to train)
cf. Extended Neural GPU cf. ByteNet cf. ConvS2S
sequential 연산 줄이는 것은 CNN을 사용하여 ENGPU, ByteNet, ConvS2S 모델의 기반을 형성, hidden representation 병렬 계산
두 개의 임의의 입출력 위치 간의 신호를 연결하는데 필요한 연산의 수는 position(위치) 간의 거리에 따라 증가함(ConvS2S는 선형적으로, $O(N)$ ByteNet의 경우 로그 형태로, $O(\log N)$ 증가)
이러한 특징은 떨어진 position 간의 dependency(의존성)을 학습하는 것을 어렵게 함 Transformer 모델은 연산이 상수 개수 $O(1)$로 줄어듦
그러나, attention 가중치를 평균화하여 effective resolution을 감소하는 문제 초래 따라서, Multi-Head Attention 사용
Self-attention(=Intra-attention)
단일 sequence 내에서 서로 다른 위치를 연결해 해당 sequence의 표현을 연산하는 attention mechanism
독해, 추상적인 요약, textual entailment(문맥적 함의), task-독립적인 문장 표현 학습에 사용됨
E2E 메모리 네트워크는 sequence 정렬 순환 대신 recurrent attention mechanism(순환 어텐션 메커니즘)을 바탕으로 하고, 간단한 언어 task에서 좋은 성능을 보임
sequence-aligned된 RNN이나 Convolution(합성곱) 방식을 사용하지 않고 입출력의 표현을 연산하는 self-attention 매커니즘에 오로지 의존하는 첫 번째 transduction model이 바로 Tranformer
cf. representation(표현) in deep learning: 어떤 task를 해결할 때, information을 어떻게 processing하여 representation 해줄지에 따라 task 난이도가 결정
cf. Attention 매커니즘 하나의 고정된 크기의 벡터에 input sequence의 모든 정보를 압축하면 정보 손실, vanishing gradient 문제
정확도 보정을 위한 기법
decoder에서 output sequence가 예측되는 매 time step마다, encoder에서 전체 입력 문장을 다시 한 번 참조(단, 해당 시점에서 예측해야할 단어와 연관 있는 input sequence에 좀 더 집중)
Query(t 시점의 decoder cell에서 hidden state)에 대해서 모든 Key(모든 time step의 encoder cell의 hidden state)
4. Model Architecture
대부분 neural transduction 모델은 seq2seq(그 중에서도 encoder-decoder) 구조 cf. seq2seq이란?
encoder는 입력 시퀀스 처리, 고정된 크기의 context vector로 변환
context vector는 encoder가 순차적으로 input sequence 처리 후 남은 마지막 hidden state로, input sequence의 단어 의미 및 순서를 요약한 정보 (수 천~만 차원의 벡터)
decoder는 context vector를 초기 state로 사용해 output sequence 생성
매 스텝마다 auto-regressive(자기 회귀적) - 이전에 생성된 symbol을 다음 symbol 생성 시 추가적인 input으로써 활용
모델의 핵심은 stacked self-attention 와 point-wise
1) Encoder & Decoder Stacks
Encoder
N=6인 동일한 layer로 구성된 stack
각 layer는 2개의 sub-layer가 있음
- Multi-head self-attention
- Position-wise Feed-Forward Network(FFN) 각 sub-layer는 잔차 연결 후 레이어 정규화
$\mathrm{Sublayer(x)}$: 각 sublayer가 수행하는 연산을 의미
모델의 모든 sub-layer+embedding-layer => 동일한 차원 유지 ($d_{model}=512$)
Decoder
N=6인 동일한 layer로 구성된 stack
Encoder와 달리 3개의 sub-layer로 구성
추가된 sub-layer: Encoder의 출력(hidden-state)을 고려한 Multi-head attention(즉, Encoder 정보를 활용해 context 반영)
- Masked
- Multi-Head Attention(w/ Encoder’s output)
- Position-wise Feed-Forward Network(FFN)
인코더와 동일하게 각 sub-alyer에 잔차 연결 후 layer 정규화 수행
Decoder에서 주목할 부분(=Masking)
We also modify the self-attention sub-layer in the decoder stack to prevent positions from attending to subsequent positions.Translation: {Decoder 스택에서 Self-attention sub-layer는 미래 position(단어)들에 attention하지 못하도록 수정하였음}
구현 방식
각 위치 $i$에서의 예측이 $i$보다 작은 위치에만 의존하도록, Output Embedding을 한 칸씩 offset하여 적용, Softmax 입력(=$QK^{T}$ 행렬)의 illegal connections를 $-\infty$로 설정해 구현. Softmax 적용하면 값이 0이 됨
2) Attention
Attention 함수란 query와 kv-pair를 output으로 매핑하는 함수
당연히 query, key, value, output은 모두 벡터
(query: 찾고자 하는 정보)
(key: 입력 데이터에서 각각의 단어에 대한 정보)
(value: 키와 연결된 실제 데이터)
output은 value의 가중치 합으로 계산, 각 값에 할당된 가중치는 값에 대응하는 key와 함께 query에 대한 compatibility function(유사도 함수)에 의해 연산됨
Scaled Dot-Product Attention
\[\mathrm{Attention(Q, K, V)=softmax(\frac{QK^T}{\sqrt{d_{k}}})V}\]1) Input은 $d_{k}$차원의 query, key 그리고 $d_{v}$차원의 value로 구성
2) 모든 key에 대한 query를 서로 내적(dot product)
cf. 왜 내적을 저렇게 표현하는가?
Q의 행과 k의 행을 내적해야 하는데, K를 열 방향으로 전치하여 곱해야 함
행렬 연산의 효율성 및 차원에 일관성 부여
왜 내적이 유사도를 나타내는가?
코사인 유사도 생각!!! 우리는 각 벡터(Q, K)의 norm 값을 알고 있을 것
내적 결과값이 커질 수록 유사할 것($\theta$ 값이 작아지니까)
3) $\sqrt{ d_{k} }$로 나눠 scaling
cf. $d_{k}$가 크면 내적 값도 커지기 때문에 softmax 함수에 넣었을 때 확률 분포가 극단적으로 변함, 뭘 넣어도 0.00000000xx 이 나오거나 0.99999999999xxx 로 극단적 치우침이 발생하면 vanishing grdient 문제가 일어남
그러면, 왜 $d_{k}$로 나누지 않았는가? 의문이 드는 게 정상
=> 내적 크기가 $d_{k}$에 비례하여 커져, 이를 조정하기 위해
=> 내적하면 Q, K의 각 요소가 예를 들어, $q_{i} \sim N(0, \sigma^2)$를 따른다고 할 때, 내적(곱)의 기대값은 분산의 곱으로 $\sigma^4$가 됨, 과소적합 문제 발생 가능성 높음
=> 벡터 norm의 기대값은 $\sqrt{ d_{k} }$에 비례, 차원 $d_{k}$가 증가할 수록 $\sqrt{ d_{k} }$만큼 증가4) softmax 함수 적용(각 값에 대한 가중치를 얻기 위함)
\[\mathrm{score(Q, K) = W_{2}\tanh(W_1{[Q;K]})}\]
cf. Addictive attention: 하나의 은닉층에서 Feed-Forward 신경망(MLP)로 유사도 계산여기서 $W_{1}$, $W_{2}$는 학습 가능한 가중치 행렬
Q, V를 concat 후, 비선형 변환을 수행해 점수 생성
왜 안 쓰냐? {matrix 연산에 매우 비효율적이기 때문임, 신경망 연산}
Dot-Product Attention은 단순 행렬 곱 연산으로 병렬 연산 최적화 가능(메모리 효율)Multi-Head Attention
single attention을 $d_{model}$차원의 Q, K, V로 수행하는 것 대신, 각 Query, Key, Value를 h번 서다른 학습 가능한 linear projection(선형 변환)을 통해 $d_{q}$, $d_{k}$, $d_{v}$차원으로 선형 투영 하는 것이 더 효과적이었음
즉, 각 Query, Key, Value를 서로 다른 학습 가능한 가중치 행렬을 통해 여러 작은 차원으로 변환시켜 h번의 scaled dot-product attention 연산을 수행한 다음 합치는 매커니즘
이 논문에서는 $h=8$, $d_{k}=d_{v}=d_{model}/h=64$로 설정
h개의 다른 attention 연산 - 병렬로 수행 (parallelization)1) Query, Key, Value를 linear-projection
\[\mathrm{head_{i}=Attention(QW_{i}^{Q}, KW_{i}^{K}, VW_{i}^{V})}\]
Query, Key, Value 행렬을 각각 h개의 서로 다른 행렬을 사용해 변환
이때, 변환을 위한 가중치 행렬은
$W_{i}^{Q} \in \mathbb{R}^{d_{model}\times{d_{k}}}$,
$W_{i}^{K} \in \mathbb{R}^{d_{model}\times{d_{k}}}$,
$W_{i}^{V} \in \mathbb{R}^{d_{model}\times{d_{v}}}$
각 attention head는 독립적으로 저차원 공간으로 투영
2) 각 Head에서 독립적으로 attention 수행Attention 함수는 각 head에 가중치 곱해진 Q, K, V 행렬을 바탕으로 당연히 위에 서술한 softmax를 적용시켜서 계산
즉, 각 Head는 서로 다른 관점(Representation Subspace)에서 정보 추출3) 모든 Head의 출력 연결(Concat), 다시 linear transformation(원래 차원인 $d_{model}$로)
\[\mathrm{MultiHead(Q, K, V) = Concat(head_{1}, \cdots, head_{h})W^O}\]변환을 위한 가중치 행렬은 $W^O \in \mathbb{R}^{hd_{v}\times d_{model}}$
추가로, Multi-Head Attention의 장점(vs. Single-Head Attention)
Single-Head Attention은 정보가 하나의 시점에서만 고려되어 다양성 부족, 모든 정보를 하나의 가중치 행렬에서만 계산하기 때문에 일종의 평균화(Averaging) 효과 발생
Multi-Head Attention은 서로 다른 h개의 Head가 다른 시점에서 정보 추출, 단어 간의 여러 관계 학습 가능, 작은 차원에서 계산하여 연산 비용 증가시키지 않고 다양한 정보 학습 가능Application of Attention in Transformer
1) Encoder-Decoder Attention (인코더-디코더 어텐션)
Transformer의 Decoder 각 layer에서 input sequence를 참고하기 위해 사용되며,
이전 시점(Layer)의 Decoder에서 생성된 Output(=Query)와 현재 시점의 Encoder가 생성한 Key, Value를 바탕으로 Decoder는 해당 인자를 활용해 Attention 함수 적용, 입력 sequence의 어떤 부분을 참고할지 결정
2) Encoder Self-Attention (인코더의 자기 어텐션)
Transformer의 Encoder 내부에서 사용되며, 이전 시점(layer)의 Encoder에서 생성된 Q, K, V를 바탕으로 각 단어가 문장 내의 다른 모든 단어와 관계를 학습(입력 sequence의 전체 구조 학습)
3) Decoder Self-Attention (디코더의 자기 어텐션)
Transformer의 Decoder 내부에서 사용되며, 이전 시점(Layer)의 Decoder에서 Q, K, V 가져옴
단, 미래 단어를 참고하지 않도록 Masking 적용
leftward information flow(I LOVE NLP. 에서 NLP->LOVE->I 순으로 단어를 참고하는 것을 생각)는 정답을 미리 보고 예측하는 문제발생.
따라서, Auto-Regressive 성질을 유지하기 위해 어텐션 가중치를 계산하는 $QK^{T}$ 행렬에서 미래 단어에 대한 값을 −∞로 설정
3) Position-wise Feed-Forward Networks
Encoder&Decoder에는 Attention과 관련된 sub-layer 말고도, FFN(Feed-Forward Network)가 존재
각 Position(=단어)에 대해 독립적이고 동일하게 적용됨, 문맥과 무관
\(\mathrm{FFN}(x)=\mathrm{max}(0, xW_{1}+b_{1})W_{2}+b_{2}\)
2개의 선형변환이 수행되는 Full Connected Layer와 1개의 ReLU 함수로 구성(->max 함수로 표현)
- 선형 변환 1 ex. 입력 벡터 $x$가 $d_{model}=512$인 차원을 가질 때, 가중치 $W_{1}$적용 후, bias $b_{1}$을 추가해 $d_{ff}=2048$로 차원 확장
- ReLU 활성화 함수 적용 ex. 4배 확장된 차원을 통해 더 많은 representation 학습
- 선형 변환 2 ex. $d_{model}=512$인 차원으로 다시 축소, 가중치 $W_{2}$적용 후, bias $b_{2}$를 추가
특징
각 position에 대해 동일한 선형 변환 적용하지만 layer마다 다른 가중치(parameters)가 사용됨
즉, 같은 레이어 내에서는 각 position에 대해 동일한 변환이 적용되지만, layer가 깊어질수록 학습된 가중치가 달라지며, 달라진 가중치 행렬이 연산에 이용됨
FFN을 합성곱(Convolution)으로 볼 수 있다.
Anther way of describing this(=Position-wise FFN) is as two convolutions with kernel size 1.
Translate: {FFN을 커널 크기가 1인 두 개의 합성곱 연산으로 설명할 수 있다.}
cf. 1x1 Conv.
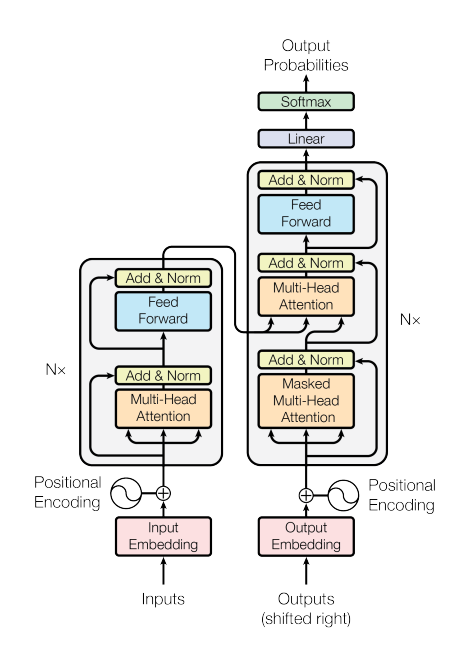
📌 Transformer Layer의 전체 구조
각 Transformer 레이어는 다음과 같은 구조로 동작:
1️⃣ Self-Attention (또는 Encoder-Decoder Attention): 각 단어가 문맥(Context)을 학습하는 단계
2️⃣ Add & Normalize (Residual Connection + Layer Normalization): 어텐션 출력과 원본 입력을 더한 후 정규화하여 안정적인 학습 유도
3️⃣ Feed-Forward Network (FFN): 각 단어의 표현을 독립적으로 변환하여 더 풍부한 특징 학습, (512 → 2048 → 512) 크기의 선형 변환 + ReLU 포함
4️⃣ Add & Normalize (Residual Connection + Layer Normalization): FFN 출력과 원본 입력을 더한 후 정규화하여 학습 안정화
4) Embeddings & Softmax
다른 sequence transduction 모델과 마찬가지로, 학습된 embedding 사용해서 입력 토큰&출력 토큰을 $d_{model}$차원 벡터로 변환
Decoder 단에서의 output vector를 다음 토큰의 확률로 변환하기 위해 선형변환과 softmax 함수 활용
두 개의 embedding layer(Input embedding & Output embedding)과 softmax 이전의 선형 변환 사이에서 동일한 가중치 행렬 공유
✔ Transformer에서는 다음과 같은 3개의 레이어에서 가중치를 공유
1️⃣ 입력 임베딩 레이어: 입력 단어를 벡터로 변환
2️⃣ 출력 임베딩 레이어: 디코더가 생성한 단어를 벡터로 변환
3️⃣ Softmax 이전의 선형 변환: 디코더 출력 벡터를 단어 분포로 변환 추가로, 임베딩 레이어에서, 위에서 서술한 가중치 행렬에 $\sqrt{ d_{model} }$을 곱하여 조정 -> 임베딩 벡터의 크기(norm 값) 조정 위해.
5) Positional Encoding
Transformer는 Recurrence X, Convolution X 이기 때문에, order information(순서 정보) 직접 활용 불가능
반드시, sequence 내에서 토큰의 상대적인 or 절대적인 position(위치 정보)을 inject 해야 함
$d_{model}$과 동일한 크기로 만들어져, input embedding과 더할 수 있음
Positional Encoding 방식
- learned 방식
- fixed 방식
- 서로 다른 주기를 가진 $\sin$ & $\cos$ 함수 채택, 짝수 차원에 sin, 홀수 차원에 cos 규칙적인 패턴 제공, 상대적 거리 정보 유지, 학습되지 않은 문장 길이에 일반화할 수 있음(extrapolate to sequence lengths longer than the ones encountered during training), learned 방법과 성능이 거의 동일
🔹 Table 1의 주요 용어 정리
| 용어 | 설명 |
|---|---|
| n | 시퀀스 길이 (입력 문장의 단어 개수) |
| d | 표현 차원 (Representation Dimension) (각 단어의 임베딩 차원, 예: d=512d=512d=512) |
| k | 컨볼루션 커널 크기 (필터 크기, 예: 3x3) |
| r | 제한된(Restricted) Self-Attention에서 고려하는 이웃 크기 |
| Complexity per Layer | 레이어의 연산량(Computational Complexity) |
| Sequential Operations | 병렬화 가능성(Sequential vs. Parallel Processing) |
| Maximum Path Length | 한 토큰에서 다른 토큰으로 정보가 전달되는 경로 길이 (짧을수록 빠른 정보 전달 가능) |
🔹 각 레이어 유형별 분석
1️⃣ Self-Attention (Transformer의 핵심)
| Layer Type | Complexity per Layer | Sequential Operations | Maximum Path Length |
|---|---|---|---|
| Self-Attention | $O(n^2 \cdot d)$ | $O(1)$ | $O(1)$ |
✔ 장점
- 모든 단어가 모든 단어를 한 번에 참조 가능 (병렬 연산 가능)
- 최대 경로 길이 = 1 → 모든 단어가 한 번의 연산으로 연결됨
- 병렬화가 가능하여 빠른 학습과 추론 가능
✔ 단점
- 연산 복잡도: $O(n2⋅d)O(n^2 \cdot d)O(n2⋅d)$ → 문장 길이가 길어질수록 계산량 급증
- 비용이 큼: 큰 문장을 다룰 때 비효율적
💡 예제:
문장 = “I love machine learning”
- “I”가 “learning”과 연관되는 경우
- Self-Attention에서는 한 번의 연산으로 연결 가능 → O(1)O(1)O(1)
2️⃣ Recurrent Layers (RNN, LSTM, GRU 등)
| Layer Type | Complexity per Layer | Sequential Operations | Maximum Path Length |
|---|---|---|---|
| Recurrent | $O(n \cdot d^2)$ | $O(n)$ | $O(n)$ |
✔ 장점
- 연산량이 O(n⋅d2)O(n \cdot d^2)O(n⋅d2)으로 Self-Attention보다 가벼움
- 메모리 사용량이 비교적 적음
✔ 단점
- 순차적(Sequential) 연산 필요 → 병렬 처리 어려움
- 최대 경로 길이 = O(n)O(n)O(n) → 먼 단어 간 관계를 학습하는데 어려움
- 긴 문장에서 장기 의존성 문제(Vanishing Gradient Problem) 발생
💡 예제:
문장 = “I love machine learning”
- “I”가 “learning”과 연관되려면 모든 단계를 거쳐야 함 → O(n)O(n)O(n)
3️⃣ Convolutional Layers (CNN 기반 NLP 모델)
| Layer Type | Complexity per Layer | Sequential Operations | Maximum Path Length |
|---|---|---|---|
| Convolutional | $O(k \cdot n \cdot d^2)$ | $O(1)$ | $O(\log_k(n))$ |
✔ 장점
- 병렬 연산 가능 → O(1)O(1)O(1)
- 경로 길이 O(logk(n))O(\log_k(n))O(logk(n)) → RNN보다 빠르게 장기 의존성을 학습 가능
✔ 단점
- 커널 크기(kkk)를 늘려야 멀리 떨어진 단어를 연결 가능
- 큰 문장을 다루려면 큰 커널 크기가 필요 → 연산량 증가
💡 예제:
문장 = “I love machine learning”
- CNN에서는 작은 필터로 학습하므로, “I”와 “learning”이 직접 연결되지 않음
- 여러 층을 거쳐야 정보가 전달됨 → O(logk(n))O(\log_k(n))O(logk(n))
4️⃣ Restricted Self-Attention (제한된 범위 내 Self-Attention)
| Layer Type | Complexity per Layer | Sequential Operations | Maximum Path Length |
|---|---|---|---|
| Restricted Self-Attention | $O(r \cdot n \cdot d)$ | $O(1)$ | $O(n/r)$ |
✔ 장점
- Self-Attention보다 연산량을 줄임 ($O(r \cdot n \cdot d)$ vs. $O(n^2 \cdot d)$)
- 병렬 연산 가능 ($O(1)$)
✔ 단점
- 제한된 범위(r) 내에서만 Self-Attention 가능 → 멀리 떨어진 단어와 연결 어려움
- 경로 길이 $O(n/r)$ → 완전한 Self-Attention보다 길어짐
💡 예제:
문장 = “I love machine learning”
- r=2r=2r=2 (이웃 단어 2개만 Attention) → “I”는 “love”와 “machine”만 참조 가능
- 더 먼 단어와 관계를 학습하려면 여러 단계 거쳐야 함 → O(n/r)O(n/r)O(n/r)
결론: Transformer(Self-Attention)가 왜 강력한가?
| Layer Type | 병렬화 가능? | 장기 의존성 학습 가능? | 연산량 |
|---|---|---|---|
| Self-Attention | ✅ 가능 ($O(1)$) | ✅ 즉시 연결 가능 ($O(1)$) | 🚨 $O(n^2 \cdot d)$ (비싸다!) |
| Recurrent (RNN, LSTM) | ❌ 불가능 ($O(n)$) | ❌ 긴 문장일수록 어려움 ($O(n)$) | ✅ $O(n \cdot d^2)$ (가볍다!) |
| Convolutional (CNN) | ✅ 가능 ($O(1)$) | ⚠ 제한적 ($O(\log_k(n))$) | ✅ $O(k \cdot n \cdot d^2)$ |
| Restricted Self-Attention | ✅ 가능 ($O(1)$) | ⚠ 제한적 ($O(n/r)$) | ✅ $O(r \cdot n \cdot d)$ |
✔ Self-Attention의 장점
- 병렬 연산 가능 → 학습 속도 빠름
- 정보 전달 경로가 1단계 → 장기 의존성 문제 해결
✔ Self-Attention의 단점
- 연산량 O(n2⋅d)O(n^2 \cdot d)O(n2⋅d) → 긴 문장에서는 너무 비싸다!
- 이를 해결하기 위해 Sparse Attention, Longformer 같은 기법이 연구됨.
4. Why Self-Attention (Self Attention vs. Recurrence/Convolution)
비교 기준(Desiderata)
- Total computational complexity per layer(layer당 총 계산 복잡도)
- The amount of computation that can be parallelized(병렬 가능 연산량)
- Long-Range Dependencies(장기 의존성 학습)
📌 Self-Attention vs. RNN
| 비교 항목 | Self-Attention | RNN (Recurrent) |
|---|---|---|
| 연산량 (Computational Complexity) | O(n²·d) | O(n·d²) |
| 병렬 처리 (Parallelization) | O(1) (전부 병렬화 가능) | O(n) (병렬화 불가능, 순차 연산) |
| 장기 의존성 학습 (Long-Range Dependencies) | O(1) (모든 토큰이 직접 연결됨, 장기 의존성 학습 용이) | O(n) (순차 연결, 장기 의존성 학습 어려움) |
📌 Self-Attention vs. CNN (Convolution)
| 비교 항목 | Self-Attention | CNN (Convolution) |
|---|---|---|
| 연산량 (Computational Complexity) | O(n²·d) | O(k·n·d²) |
| 병렬 처리 (Parallelization) | O(1) (전부 병렬화 가능) | O(1) (병렬화 가능하지만 커널 크기에 따라 제한됨) |
| 장기 의존성 학습 (Long-Range Dependencies) | O(1) (모든 토큰이 직접 연결됨) | O(logₖ(n)) (Dilated CNN 사용 시 여러 층 필요함) |
- CNN은 한 번에 볼 수 있는 토큰 개수가 제한되므로, 여러 층을 쌓아야 장기 의존성을 학습할 수 있음
- Dilated CNN을 사용하면 O(logₖ(n))로 줄어들지만, 여전히 Self-Attention보다 연결 경로가 길어 학습이 불리함
즉, self-attention은 RNN, CNN과 비교했을 때, 시퀀스 길이가 길어지면 연산량이 커지는 문제가 발생하기 때문에 제한된 범위($r$) 내에서만 Self-attention을 수행하는 Restricted Self-Attention을 고려
- O(n²·d)에서 O(n·r·d)로 연산량 감소
- 최대 경로 길이(Path Length)가 O(n/r)로 감소 (=멀리 있는 단어를 보려면 여러 단계를 거쳐야 하는데, 연산량을 줄일 수 있음)
5. Training
✅ 1. 학습 데이터 & 배치 구성 (Training Data and Batching)
📌 (1) 사용된 데이터셋
| 언어 조합 | 문장 개수 | 토큰화 방식 | 어휘 크기 |
|---|---|---|---|
| WMT 2014 영어-독일어 (EN-DE) | 4.5M (450만 문장) | Byte-Pair Encoding (BPE) | 약 37,000개 |
| WMT 2014 영어-프랑스어 (EN-FR) | 36M (3,600만 문장) | WordPiece | 32,000개 |
🔹 Byte-Pair Encoding (BPE): 희귀 단어를 단어 조각(Subword)으로 나누어 어휘 크기를 줄이고 희귀성을 해결하는 방법
🔹 WordPiece: BPE와 유사한 기법으로, 토큰을 조합하여 단어를 생성하는 방식
📌 (2) 배치 구성
- 문장 길이를 고려하여 배치(Batching) 구성
→ 비슷한 길이의 문장들을 하나의 배치로 묶어 패딩 비용을 최소화 - 배치 크기: 한 번의 학습 단계에서 약 25,000개의 원문 토큰 + 25,000개의 번역문 토큰을 처리
✅ 2. 하드웨어 & 학습 일정 (Hardware and Training Schedule)
Transformer 모델의 학습은 8개의 NVIDIA P100 GPU에서 수행되었습니다.
여기서 Base 모델과 Big 모델의 학습 시간 차이를 확인할 수 있습니다.
| 모델 | 학습 스텝 (Steps) | 스텝당 시간 | 총 학습 시간 |
|---|---|---|---|
| Transformer (Base) | 100,000 | 0.4초 | 약 12시간 |
| Transformer (Big) | 300,000 | 1.0초 | 약 3.5일 |
✅ 3. Optimizer
📌 (1) Adam Optimizer 사용
- Transformer는 Adam 최적화 알고리즘을 사용
- Adam의 모멘텀 계수(β1, β2)와 학습률 조정 파라미터는 아래와 같음
- β1 = 0.9, β2 = 0.98, ϵ = 10⁻⁹
- 모멘텀과 이동평균을 고려해 기울기 업데이트를 부드럽게 진행
📌 (2) 학습률 스케줄링 (Learning Rate Scheduling)
Transformer는 고정 학습률을 사용하지 않고, 특정 규칙에 따라 변하는 학습률을 사용함. 학습률 계산 공식:
$lrate = d_{model}^{-0.5} \times \min(step_num^{-0.5}, step_num \times warmup_steps^{-1.5})$
- 학습 초반에는 학습률을 선형적으로 증가 (step_num < warmup_steps)
- 특정 스텝 이후에는 학습률을 감소 (step_num > warmup_steps)
- Warmup 스텝(warmup_steps) = 4000 (초반 4000 스텝 동안 학습률 증가) ✅ 4. 정규화 기법 (Regularization Techniques) Transformer 모델은 과적합(Overfitting) 방지를 위해 3가지 정규화 기법을 사용
📌 (1) 드롭아웃 (Dropout)
- 각 서브 레이어의 출력에 대해 드롭아웃 적용
- 임베딩 + 위치 인코딩(Position Encoding) 합산 후에도 드롭아웃 적용
- 드롭아웃 비율 Pdrop=0.1P_{drop} = 0.1Pdrop=0.1 사용
→ 10%의 뉴런을 무작위로 꺼서 과적합 방지
📌 (2) 레이블 스무딩 (Label Smoothing)
- 레이블 스무딩은 정확한 정답(label) 대신, 약간의 확률 분포를 가지도록 변형하는 기법
- 예를 들어,
- 기존: 정답 라벨 → 100% 확률로 해당 클래스 선택
- 변형: 정답 라벨 확률을 90%로 줄이고, 나머지를 다른 클래스에 분배
📌 (3) 잔차 연결 + Layer Normalization (Residual Connection + Layer Norm)
- Transformer는 각 서브레이어(Sub-layer)에서 “Residual Connection”을 적용한 후, Layer Normalization을 수행
- 이는 모델이 더 깊어져도 학습이 안정적으로 이루어지도록 보장
- 수식으로 표현하면: $\text{Output} = \text{LayerNorm}(X + \text{Sublayer}(X))$ 여기서 X는 입력, Sublayer(X)는 Self-Attention이나 Feed-Forward Network의 출력 이 방식이 중요한 이유?
- 잔차 연결(Residual Connection): 기울기 소실(Vanishing Gradient) 문제를 방지
- Layer Normalization: 각 레이어의 출력 분포를 정규화하여 안정적인 학습을 유도
🔹 장점:
- 모델이 너무 확신하지 않도록 만들어 과적합을 방지
- BLEU 점수를 향상시키는 효과 있음
6. Result
기계 번역(Machine Translation) 성능이 기존 SOTA 대비 향상됨
Dropout, Multi-Head Attention, 모델 크기 등 하이퍼파라미터의 영향 분석
Constituency Parsing에서도 강력한 성능을 보이며, 번역 이외의 NLP Task에도 효과적
Transformer는 다양한 구조적 실험을 통해 최적의 설정을 찾았으며, 기존 모델보다 효율적이고 해석 가능한 모델임