Post

Concepts of Programming Languages 03: Describing Syntax and Semantics

Posted Updated
Ambiguous Expression Grammar
Ambiguous Expression Grammar
By Youngbeom Cho
views 12 min read

1. Intro

Syntax(구문): 프로그래밍 언어의 문법이나 구조를 의미

Semantics(의미론): Syntax에 대한 의미

  • Syntax와 Semantics는 언어의 정의를 제공한다.

  • 잘 설계된 언어라면 그 의미는 구문으로부터 파악이 가능해야 한다.

  • Sentence: alphabet으로 구성된 문자열
  • Language: Sentences(문장)의 집합
  • Lexeme(어휘): 가장 낮은 수준의 구문 단위 (ex. *, sum, begin)
  • token: 어휘의 카테고리 (ex. identifier)

[Lexeme와 Token 구분 예시]
index = 2 * count + 17;

LexemesTokens
indexidentifier
=equal_sign
2int_literal
*mult_op
countidentifier
+plus_op
17int_literal
;semicolon

2. BNF & Context-Free Grammers

BNF(Backus-Naur Form)은 Context-Free Grammers와 동일한 의미이다.

BNF란 놈 촘스키에 의해 개발된 문맥 자유 언어이며, context에 상관 없이 동일하게 해석되는 문법을 가진 언어를 말한다.
즉, 반드시 하나의 문장이 하나의 의미를 지녀야 한다.

BNF Fundamentals

  1. Terminal: lexeme나 token을 칭하는 용어이다.
  2. Non-Terminal: Terminal이 아닌 것을 의미하며, ‘<>’(angle brackets)에 싸여있다.
  3. 규칙은 LHS(Left-Hand-Side)와 RHS(Right-Hand-Side)로 구성된다. 예를 들어, <assign> → <id> = <expr>이라는 규칙이 존재하면 LHS는 <assign>이며, RHS는 <id> = <expr> 이다. LHS는 무조건 Non-Terminal이 와야 하며, RHS는 하나 이상의 Non-Terminal, Terminal이 모두 올 수 있다.
    <stmt> -> <single_stmt> | begin <stmt_list> end와 같은 표현이 가능하다. 해당 규칙의 의미는 <stmt>이라는 nonterminal이 single_stmt라는 nonterminal로 확장되거나, begin <stmt_list> end라는 nonterminal과 terminal의 조합으로 확장될 수 있다는 의미이다.
    또한, Syntactic list는 recursion을 이용해 설명할 수 있다. <ident_list> → ident | ident, <ident_list>는 대표적으로 재귀로 표현된 예시이다.
  4. 문법은 이러한 규칙들의 공집합이 아닌 유한 집합으로 표현된다.
  5. Start Symbol은 처음 derivation이 시작되는 Non-Terminal을 말한다.

3. Parse Tree & Ambiguity in Grammers

Derivation

보통은 전개라고 번역하며, symbol로 이뤄진모든 문자열은 sentential form을 가진다고 말한다.
sentential form이란 정확히는 전개 중간에 터미널과 논터미널이 섞여 나오는 모든 문자열을 말한다.
Sentence(문장)이란 꺽새가 없는 터미널 symbol로만 이뤄진 문자열을 말한다.
Leftmost Derivation이란 좌우선유도 방식이라 번역하며, 좌측부터 Non-Terminal을 sentential form으로 바꿔주는 것을 말한다.

Parse Tree

Derivation을 트리 구조의 형태로 계층적인 표현으로 나타낸 것을 파스 트리라고 한다.

Ambiguity in Grammars

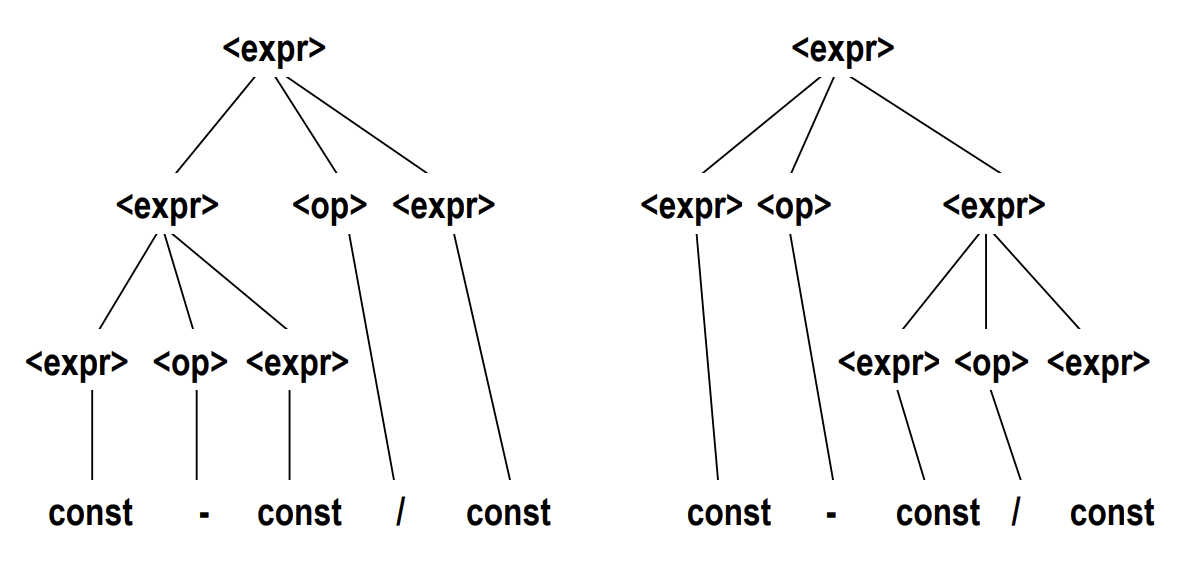
문법이 모호하다는 의미는 동일한 sentential form(문장 형태)를 가지고 있지만 derivation 과정이 달라 파스 트리의 구조가 다른 형태가 두 가지 이상 존재하는 경우를 말한다. (단, 이를 증명하기 위해 좌우선유도, 우우선유도 방법 중 하나만을 선택에 적용해줘야 한다.)

게시글 미리보기 이미지에 올려놓은 이미지가 바로 문법의 모호성을 증명하는 파스 트리이다.

문법의 모호성을 줄이는 방법

  1. 연산자 우선순위를 적용하면 모호성이 사라진다.(Precedence Cascade)
    구체적으로, <expr> → <expr> <op> <expr> | const과 <op> → / | -로 이뤄진 문법보다는,
    <expr> → <expr> - <term> | <term>, <term> → <term> / const | const와 같이 op에 순서를 부여하는 것이 하나로 결정되는 파스 트리를 생성할 수 있다.
  2. 연산자 우선순위를 적용하더라도 모호성이 존재하는 경우가 있는데, 이때는 ‘결합법칙’을 활용한다.
    구체적으로, <expr> → <expr> + <expr> | const보다는 <expr> → <expr> + const를 통해 모호성을 줄일 수 있다.
    즉, non-terminal symbol로만 표현하기 보다는 terminal symbol을 사용하여 파스 트리를 무조건적으로 왼쪽 아니면 오른쪽에서 만들어지게 한다.

4. EBNF

Extend-BNF는 기존 BNF로 작성되는 문법 중 불편함을 덜기 위해서 확장한 BNF이다.

  • 선택적인 부분이 존재한다면, []으로 표현한다.
  • 두 터미널 또는 논터미널 중에 선택하는 상황이라면 ()괄호와기호를 이용한다.
  • 0번 이상의 반복을 나타낼 때는 {}중괄호를 사용한다.
    예를 들어, BNF에서 <expr> → <expr> + <term> | <expr> - <term> | <term>이라는 문법이 사용되었다면,
    EBNF로는 <expr> → <term> {(+|-) <term>}으로 간결한 표현이 가능해진다.

5. Semantics

의미론이라고 해석한다. Syntax(문법)은 언어의 틀, 규칙을 생성하였다면, 문장의 의미를 형성하는 Semantics가 필요하다.

프로그래밍 언의의 의미론에 대해서 다음 세 가지 접근 방식이 있었다.

Operational Semantics

연산의미론이라고 번역한다. 문장을 번역하기보다는, “언어의 구현”에 집중하며, 문장을 추상적인 기계에 실행시킴으로써 그 프로그램의 의미(semantics)를 기술하는 방법론이다.

  • 실제 프로그램의 실행을 통해 의미를 부여하지만, 언어 구현 단계에서는 실제 돌릴 기계가 없기 때문에 가상으로 실행한다.
  • 고급언어에 해당 방법론을 사용하기 위해서 virtual machine이 필요하다.

Axiomatic Semantics

공리의미론이라고 번역한다. 구문에 적용되는 수학적, 논리적 공리를 설명함으로써 언어에 의미(Semantics)를 부여하는 방법론이다.

  • 세 가지 방법론 중 가장 추상적인 방법이다.
  • 그것의 의미는 몇 가지 논리를 포함한 무언가에 의해 명확하게 증명되어질 수 있어야 한다.
  • formal logic이라는 미적분학의 한 분야에 기반하며, 형식적인 프로그램을 증명하는 것이 원래 목적이다.
  • 공리나 규칙은 언어가 제공하는 statement type에 의해 정의된다.
  • logic expression은 assertion(단언)이라고 부른다.
  • statement 전에 등장하는 assertion(단언)은 실행 중에 참이되는 변수들 내에서의 관계와 제약을 보여준다.
  • statement를 따르는 assertion은 postcondition이라고 한다.
  • 가장 약한 precondition(사전조건)은 사후조건을 보장하는 가장 억제력이 덜한 사전조건을 의미한다.
  • 예를 들어서, a = b + 1(a > 1)에서 가능한 b의 precondition은 b>9, b>10, b>11 등이 있을 것이다. 그 중에서 가장 제약을 덜 받는 Weakest precondition은 b > 0이다.

[Program Proof Process]
실제 프로그램을 검증할 때, 잘 짜여졌는지를 판단하는 과정이 있다.
전체 프로그램에 대한 사후조건이 다음과 같은 결과를 만족해야 한다.

마지막 문장의 사후조건이 원하는 결과를 도출한다면,
마지막 문장의 사후조건을 만족하는 가장 작은 사전조건을 계산한다.
마지막 문장의 사후조건을 만족하는 가장 작은 사전조건은 (마지막 문장 - 1)번째 문장의 사후조건이다.
…(이러한 방식을 이어나가다가)
첫 번째 문장의 사전조건이 “프로그램 명세”와 같다면,
만든 프로그램이 올바르다고 판단한다.

[추가]
S1;S2와 같은 형태로 sequence에 대한 참조 규칙이 있다면, P1을 S1의 사전조건, P2를 S1의 사후조건, P2를 S2의 사전조건, P3를 S3의 사후조건이라고 가정했을 때,
{P1}S1{P2}
{P2}S2{P3}
라는 표현을 하며,
연결된 문장의 경우 공리를 사용하지 못해 추론 규칙을 사용한다.

{P1}S1;S2{P3}

Denotational Semantics

표기의미론이라고 번역한다. 프로그램의 수식이나 문장의 의미를 수학적 함수 형태로 정의하여 의미(Semantics)를 설명하는 방법론이다.

Computer Science, Concepts of Programming Languages
Programming Languages Syntax
This post is licensed under CC BY 4.0 by the author.